题目内容
如图，EO⊥CO，∠BOC=2∠AOC，求∠BOE=考点：垂线
专题：
分析：首先根据邻补角的性质和∠BOC=2∠AOC可得∠BOC=120°，再根据垂线定义可得∠COE=90°，然后再计算出∠BOE的度数即可．
解答：解：∵∠BOC=2∠AOC，∠AOC+∠BOC=180°，
∴∠BOC=120°，
∵EO⊥CO，
∴∠COE=90°，
∴∠BOE=120°-90°=30°，
故答案为：30．
解：∵∠BOC=2∠AOC，∠AOC+∠BOC=180°，∴∠BOC=120°，
∵EO⊥CO，
∴∠COE=90°，
∴∠BOE=120°-90°=30°，
故答案为：30．
点评：此题主要考查了垂线，关键是掌握垂线的定义：当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线．
练习册系列答案
相关题目
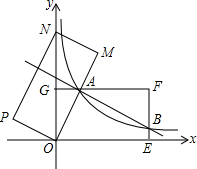如图，在平面直角坐标系xOy中，矩形OEFG的顶点E的坐标为（4，0），顶点G的坐标为（0，2），将矩形OEFG绕点O逆时针旋转，使点F落在y轴的点N处，得到矩形OMNP，OM与GF交于点A．已知
=
，则
的值是（ ）
| b |
| a |
| 5 |
| 13 |
| a+b |
| a-b |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，O为直线AB上的一点，OE，OF分别平分∠AOC，∠COB，请问OE⊥OF吗？为什么？
如图，点A、E、F、C线上，AD∥BC，AD=CB，AE=CE，求证：∠B=∠D．当地面高于海平面1米时，记作“+1米”，那么地面低于海平面10米时，记作（ ）
| A、-1米 | B、+1米 |
| C、-10米 | D、+10米 |
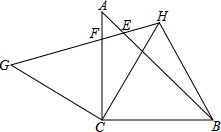△ABC中，∠ACB=90°，AC=BC=1，将△ABC绕点C逆时针旋转角α（0＜α＜90°）得△GHC，连结BH、CH．CH交AB于点D，GH交AB、AC于点E、点F．