题目内容
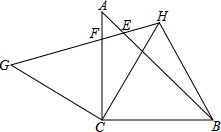 △ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转角α(0<α<90°)得△GHC,连结BH、CH.CH交AB于点D,GH交AB、AC于点E、点F.
△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转角α(0<α<90°)得△GHC,连结BH、CH.CH交AB于点D,GH交AB、AC于点E、点F.(1)在图中不添加其它任何线段的情况下,请你找出一对全等三角形,并加以证明.(△ABC与△GHC全等除外)
(2)当△BHD是等腰三角形时,求α.
考点:全等三角形的判定与性质
专题:
分析:(1)依据全等三角形的判定,可找出全等的三角形有:△CBD≌△CGF或△AEF≌△HED或△ACD≌△HCF等.由旋转的意义可证∠GCF=∠BCD,GC=BC,∠G=∠CBD=45°,所以△CBD≌△CGF.
(2)当△BBD是等腰三角形时,要分别讨论HB=HD、BH=BD、HD=DB三种情况,第一,三种情况不成立,只有第二种情况成立,求得α=30°.
(2)当△BBD是等腰三角形时,要分别讨论HB=HD、BH=BD、HD=DB三种情况,第一,三种情况不成立,只有第二种情况成立,求得α=30°.
解答:解:如图所示,
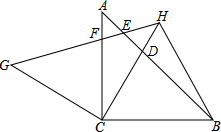
(1)全等的三角形有:△CBD≌△CGF或△AEF≌△HED或△ACD≌△HCF等;
以证△CBD≌△CGF为例:
证明:∵∠ACH+∠GCF=∠ACH+∠BCD=90°,
∴∠GCF=∠BCD,
∵GC=BC,
∴∠G=∠CBD=45°,
∴△CBD≌△CGF;
(2)在△CBH中,
∵CB=CH,
∴∠CBH=∠CHB=
(180°-α),
又∵△ABC是等腰直角三角形,
∴∠ABC=45°,
①若HB=HD,则∠HDB=∠HBD,
∵∠HDB=45°+α,
∠HBD=∠CBH-45°=
(180°-α)-45°=45°-
,
∴45°+α=45°-
,
∴α=0°(舍去);
②∵∠BHC=∠HBC>∠HBD,
∴BD>HD,即BD≠HD;
③若BH=BD,则∠BDH=∠BHD,
即45°+α=
(180°-α),
∴α=30°,
由①②③可知,当△BHD为等腰三角形时,α=30°.

(1)全等的三角形有:△CBD≌△CGF或△AEF≌△HED或△ACD≌△HCF等;
以证△CBD≌△CGF为例:
证明:∵∠ACH+∠GCF=∠ACH+∠BCD=90°,
∴∠GCF=∠BCD,
∵GC=BC,
∴∠G=∠CBD=45°,
∴△CBD≌△CGF;
(2)在△CBH中,
∵CB=CH,
∴∠CBH=∠CHB=
| 1 |
| 2 |
又∵△ABC是等腰直角三角形,
∴∠ABC=45°,
①若HB=HD,则∠HDB=∠HBD,
∵∠HDB=45°+α,
∠HBD=∠CBH-45°=
| 1 |
| 2 |
| α |
| 2 |
∴45°+α=45°-
| α |
| 2 |
∴α=0°(舍去);
②∵∠BHC=∠HBC>∠HBD,
∴BD>HD,即BD≠HD;
③若BH=BD,则∠BDH=∠BHD,
即45°+α=
| 1 |
| 2 |
∴α=30°,
由①②③可知,当△BHD为等腰三角形时,α=30°.
点评:本题考查了全等三角形的判定,综合应用直角三角形性质解直角三角形,进行逻辑推理能力和运算能力.

练习册系列答案
相关题目
a、b是两个有理数,若a-b<0,那么关于a、b的说法一定正确的是( )
| A、a<0,b<0 |
| B、a<0,b>0 |
| C、a>0,b<0 |
| D、a<b |
下列图形中,正确表示△ABC中BC边上的高的是( )
A、 |
B、 |
C、 |
D、 |
 如图,EO⊥CO,∠BOC=2∠AOC,求∠BOE=
如图,EO⊥CO,∠BOC=2∠AOC,求∠BOE=
 如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.
如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.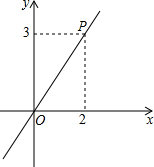 如图,已知正比例函数y=kx经过点P,
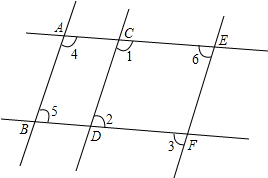
如图,已知正比例函数y=kx经过点P, 如图,直线a、b、c被直线l所截,如果∠1=∠2=65°,且直线b∥c,那么直线a与c平行吗?∠3等于多少度?
如图,直线a、b、c被直线l所截,如果∠1=∠2=65°,且直线b∥c,那么直线a与c平行吗?∠3等于多少度?