题目内容
一个矩形ABCD的较短边长为2.
(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.

(1)如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;
(2)如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.

考点:相似多边形的性质
专题:
分析:(1)由题意可知矩形DMNC与矩形ABCD相似,根据相似多边形对应边的比相等列出比例式,就可以得到它的另一边长;
(2)根据相似矩形对应边成比例列出比例式求出DF的长,再根据矩形面积公式求解即可.
(2)根据相似矩形对应边成比例列出比例式求出DF的长,再根据矩形面积公式求解即可.
解答:解:(1)由已知得MN=AB=2,MD=
AD=
BC,
∵沿长边对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似,
=
,
∴DM•BC=AB•MN,即
BC2=4,
∴BC=2
,即它的另一边长为2
;
(2)∵矩形EFDC与原矩形ABCD相似,
∴
=
,
∵AB=CD=2,BC=4,
∴DF=
=1,
∴矩形EFDC的面积=CD•DF=2×1=2.
| 1 |
| 2 |
| 1 |
| 2 |
∵沿长边对折后得到的矩形与原矩形相似,
∴矩形DMNC与矩形ABCD相似,
| DM |
| AB |
| MN |
| BC |
∴DM•BC=AB•MN,即
| 1 |
| 2 |
∴BC=2
| 2 |
| 2 |
(2)∵矩形EFDC与原矩形ABCD相似,
∴
| DF |
| AB |
| CD |
| BC |
∵AB=CD=2,BC=4,
∴DF=
| AB•CD |
| BC |
∴矩形EFDC的面积=CD•DF=2×1=2.
点评:本题考查相似多边形的性质:相似多边形对应边的比相等.也考查了矩形的面积.

练习册系列答案
相关题目
一个多边形的内角和是外角和的3倍,则这个多边形是( )
| A、五边形 | B、六边形 |
| C、七边形 | D、八边形 |
 如图所示,矩形ABCD中,AB=4,AD=
如图所示,矩形ABCD中,AB=4,AD=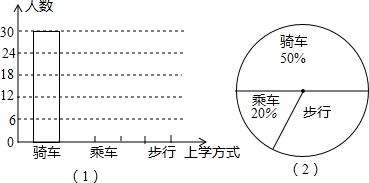
 如图,EO⊥CO,∠BOC=2∠AOC,求∠BOE=
如图,EO⊥CO,∠BOC=2∠AOC,求∠BOE=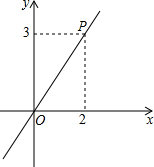 如图,已知正比例函数y=kx经过点P,
如图,已知正比例函数y=kx经过点P,