题目内容
6.我们知道多项式的乘法,可以利用图形的面积进行解释,如:(2a+b)(a+b)=2a2+3ab+b2就可以用图1、图2等图形的面积表示.(1)请你写出图3所表示的一个等式:(a+2b)(2a+b);
(2)试画出一个几何图形,使它的面积能表示为(a+3b)(a+b)=a2+4ab+3b2;
(3)请仿照上述方法另写一个只含有a,b的等式,并画出与之对应的图形.
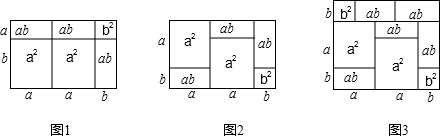
分析 (1)根据长方形的面积=长×宽,即可解决问题.
(2)画一个长为(a+3b),宽为(a+b)的长方形即可.
(3)任意写一个一个只含有a,b的等式,根据长方形的面积公式,确定长与宽,再利用分割法画出图形即可.
解答 解:(1)由图3可知长方形的面积=(a+2b)(2a+b),
故答案为(a+2b)(2a+b).
(2)(a+3b)(a+b)=a2+4ab+3b2可以用图4表示,
(3)(a+b)(a+2b)=a2+3ab+2b2可以用图5表示,
点评 本题考查多项式乘多项式,长方形的面积等知识,解题的关键是理解题意,是数形结合的好题目,这里的等式左右两边分别表示长方形的面积的两种求法,属于中考创新题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.化简|x-5|-|2x-13|(5<x<6)得( )
| A. | -x+8 | B. | 3x-18 | C. | -3x+18 | D. | x-8 |
18. 某校八(1)班进行“品学兼优生”的推选工作,经过自荐和第一轮筛选后,甲、乙两名同学进入终选.下表为甲、乙两位同学的得分情况.其中人气分的计算办法是:根据班级同学和部分老师的投票结果,同学一票记3分,老师一票记10分,两个分数相加即为人气分.
某校八(1)班进行“品学兼优生”的推选工作,经过自荐和第一轮筛选后,甲、乙两名同学进入终选.下表为甲、乙两位同学的得分情况.其中人气分的计算办法是:根据班级同学和部分老师的投票结果,同学一票记3分,老师一票记10分,两个分数相加即为人气分.
(1)求甲的人气分m的值;
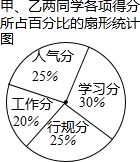
(2)经全班同学讨论决定,候选人的最后得分根据如图所示的百分比计算总分,总分高的人被选上,请你判断谁被选上,并说明理由.
 某校八(1)班进行“品学兼优生”的推选工作,经过自荐和第一轮筛选后,甲、乙两名同学进入终选.下表为甲、乙两位同学的得分情况.其中人气分的计算办法是:根据班级同学和部分老师的投票结果,同学一票记3分,老师一票记10分,两个分数相加即为人气分.
某校八(1)班进行“品学兼优生”的推选工作,经过自荐和第一轮筛选后,甲、乙两名同学进入终选.下表为甲、乙两位同学的得分情况.其中人气分的计算办法是:根据班级同学和部分老师的投票结果,同学一票记3分,老师一票记10分,两个分数相加即为人气分. | 候选人 | 人气分 | 学习分 | 行规分 | 工作分 | ||
| 同学投票 | 老师投票 | 分数 | ||||
| 甲 | 25 | 2 | m | 94 | 93 | 95 |
| 乙 | 22 | 3 | 96 | 98 | 90 | 90 |
(2)经全班同学讨论决定,候选人的最后得分根据如图所示的百分比计算总分,总分高的人被选上,请你判断谁被选上,并说明理由.
 如图,在长方形ABCD中,边AB、BC的长(AB<BC)是方程x2-7x+12=0的两个根,点P从点A出发,以每秒1个单位的速度沿△ABC边A→B→C→A的方向运动,运动时间为t(秒).
如图,在长方形ABCD中,边AB、BC的长(AB<BC)是方程x2-7x+12=0的两个根,点P从点A出发,以每秒1个单位的速度沿△ABC边A→B→C→A的方向运动,运动时间为t(秒). 如图,要使得△ABC≌△DFE,已知∠A=∠D,AB=DF,根据AAS还需要的条件是∠ACB=∠DEF.
如图,要使得△ABC≌△DFE,已知∠A=∠D,AB=DF,根据AAS还需要的条件是∠ACB=∠DEF.