题目内容
14.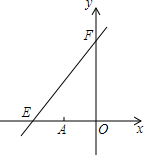 如图,直线y=kx+6与x轴,y轴分别交于点E,F,点E的坐标为(-8,0),点A的坐标是(-6,0).
如图,直线y=kx+6与x轴,y轴分别交于点E,F,点E的坐标为(-8,0),点A的坐标是(-6,0).(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)在直线EF上是否存在另外的点Q,使得△OQA的面积为12?若存在,请求出点Q的坐标;若不存在,说明理由.
分析 (1)根据待定系数法,可得k值;
(2)根据点在直线上,可得P点坐标,根据三角形的面积公式,可得函数解析式;再根据P(x,y)是第二象限内的直线上,可得自变量的取值范围;
(3)根据点在直线上,可得点Q坐标(x,$\frac{3}{4}$x+6),根据三角形的面积,可得关于x的方程,根据解方程,可得x的值,根据自变量与函数值的对应关系,可得Q点坐标.
解答 解:(1)把E(-8,0)代入直线y=kx+6中,得
0=-8k+6,
解得:k=$\frac{3}{4}$;
(2)P在直线是:y=$\frac{3}{4}$x+6,
设P坐标是:(x,$\frac{3}{4}$x+6)
S△OPA=$\frac{1}{2}$×|OA|×($\frac{3}{4}$x+6)
=$\frac{1}{2}$×6×($\frac{3}{4}$x+6)
=$\frac{9}{4}$x+18,
P是第二象限内的直线上的一个动点,得
-8<x<0.
∴OPA的面积S与x的函数关系式为s=$\frac{9}{4}$x+18,
自变量的取值范围为-8<x<0;
(3)Q在直线是:y=$\frac{3}{4}$x+6,
设Q坐标是:(x,$\frac{3}{4}$x+6),
S=$\frac{1}{2}$×|OA|×($\frac{3}{4}$x+6)=$\frac{1}{2}$×6×($\frac{3}{4}$x+6)=$\frac{9}{4}$x+18=12,
$\frac{9}{4}$x+18=12,
解得
x=-$\frac{8}{3}$,
当x=-$\frac{8}{3}$时,y=$\frac{3}{4}$×(-$\frac{8}{3}$)+6=4
即当Q点的坐标是(-$\frac{8}{3}$,4)时,△OQA的面积为12.
点评 本题考查了一次函数综合题,利用了待定系数法求函数解析式,利用点在直线上得出点的坐标(x,$\frac{3}{4}$x+6),利用三角形的面积公式是求函数关系式的关键.

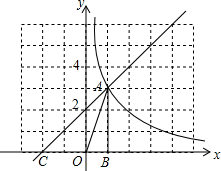 如图,在平面直角坐标系中,直线y=x+$\frac{1}{2}m$的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限内交于点A,与x轴交于点C,AB垂直于X轴,垂足为B,且三角形AOB的面积为1.
如图,在平面直角坐标系中,直线y=x+$\frac{1}{2}m$的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限内交于点A,与x轴交于点C,AB垂直于X轴,垂足为B,且三角形AOB的面积为1.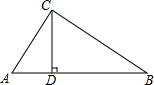 在Rt△ABC中,∠C=90°,CD是斜边AB的高.已知CD=5,sinB=$\frac{1}{3}$.求BC、BD、AD、AC的长以及tanA、cos∠ACD的值.
在Rt△ABC中,∠C=90°,CD是斜边AB的高.已知CD=5,sinB=$\frac{1}{3}$.求BC、BD、AD、AC的长以及tanA、cos∠ACD的值.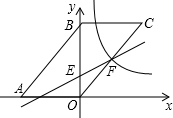 如图,在平面直角坐标系中,四边形ABCO是平行四边形,A点坐标(-6,0),B点坐标(0,6),点C在第一象限,直线y=$\frac{1}{2}$x+2与y轴交与点E,与OC交与点F,反比例函数y=$\frac{k}{x}$(x>0)经过点F.
如图,在平面直角坐标系中,四边形ABCO是平行四边形,A点坐标(-6,0),B点坐标(0,6),点C在第一象限,直线y=$\frac{1}{2}$x+2与y轴交与点E,与OC交与点F,反比例函数y=$\frac{k}{x}$(x>0)经过点F.