题目内容
19.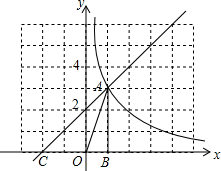 如图,在平面直角坐标系中,直线y=x+$\frac{1}{2}m$的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限内交于点A,与x轴交于点C,AB垂直于X轴,垂足为B,且三角形AOB的面积为1.
如图,在平面直角坐标系中,直线y=x+$\frac{1}{2}m$的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限内交于点A,与x轴交于点C,AB垂直于X轴,垂足为B,且三角形AOB的面积为1.(1)求m的值;
(2)求三角形ABC的面积.
分析 (1)根据反比例函数y=$\frac{k}{x}$系数k的几何意义即可求得m的值;
(2)根据直线y=x+1求得C的坐标,解两个解析式组成的方程组求得A的坐标,然后根据三角形面积求得即可.
解答 解:(1)∵点A是反比例函数y=$\frac{m}{x}$的图象的点,AB垂直于X轴,垂足为B,且三角形AOB的面积为1.
∴S△AOB=$\frac{1}{2}$m,
∵三角形AOB的面积为1.
∴m=2;
(2)∵m=2,
∴直线y=x+1,
令y=0,则x=-1,
∴C(-1,0),
∴OC=1,
解$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{2}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$,
∴A(1,2),
∴三角形ABC的面积=$\frac{1}{2}$(1+1)×2=2.
点评 本题考查了反比例函数和一次函数的交点问题,根据反比例函数y=$\frac{k}{x}$系数k的几何意义,求得m的值是解题的关键.

练习册系列答案
相关题目
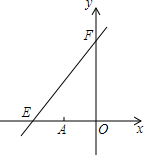 如图,直线y=kx+6与x轴,y轴分别交于点E,F,点E的坐标为(-8,0),点A的坐标是(-6,0).
如图,直线y=kx+6与x轴,y轴分别交于点E,F,点E的坐标为(-8,0),点A的坐标是(-6,0).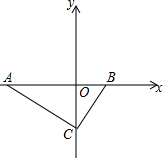 如图,在平面直角坐标系中,点A在x轴的负半轴上,点B在x轴的正半轴上.C在y轴的负半轴上,AC所在直线为y=kx-12.AC⊥BC.BC的长的$\frac{1}{3}$倍是方程x2-3x-10=0的根.
如图,在平面直角坐标系中,点A在x轴的负半轴上,点B在x轴的正半轴上.C在y轴的负半轴上,AC所在直线为y=kx-12.AC⊥BC.BC的长的$\frac{1}{3}$倍是方程x2-3x-10=0的根.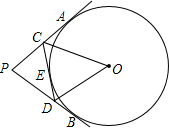 如图,PA,PB切⊙O于点A,B,点E是劣弧$\widehat{AB}$上一点,过E点作⊙O的切线交PA与C,交PB于D,若∠P=80°,∠DOC=50°.
如图,PA,PB切⊙O于点A,B,点E是劣弧$\widehat{AB}$上一点,过E点作⊙O的切线交PA与C,交PB于D,若∠P=80°,∠DOC=50°.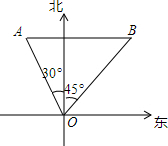 如图,某海防哨所(O)发现在它的北偏西30°,距离为500m的A处有一艘船,该船向正东方向航行,经过3min到达哨所东北方向的B处,则该船的航速为每小时13.7km.(精确到0.1)
如图,某海防哨所(O)发现在它的北偏西30°,距离为500m的A处有一艘船,该船向正东方向航行,经过3min到达哨所东北方向的B处,则该船的航速为每小时13.7km.(精确到0.1)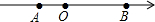 已知数轴上A,B对应的实数为a,b,化简代数式:|a-b|-$\sqrt{(b-a)^{2}}$+$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=b-a.
已知数轴上A,B对应的实数为a,b,化简代数式:|a-b|-$\sqrt{(b-a)^{2}}$+$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=b-a.