题目内容
2.某公司销售某种商品,其标价为100元,现在打6折销售仍然获利50%,为扩大销量,公司决定在打6折的基础上再降价,规定顾客每再多买1件,顾客购买的所有商品的单价再少1元,但不能出现亏损的情况,设顾客购买商品件数为x(件),公司获得利润为W(元)(1)求该商品的进价是多少元?
(2)求W与x的函数关系式并求公司销售利润最大值?
(3)公司发现x在某一范围内会出现顾客购买件数越多公司利润反而越少的情况,为避免出现这种情况,应规定最低售价为多少元?
分析 (1)根据某公司销售某种商品,其标价为100元,现在打6折销售仍然获利50%,可以列出相应的方程,从而可以解答本题;
(2)根据题意可以得到W与x的函数关系式,将W与x的函数关系式化为顶点式,即可求得最大值;
(3)由第(2)问的函数关系式,再根据本问提供的信息可以解答本题.
解答 解:(1)设商品的进价为x元,根据题意可得
100×0.6=x(1+50%),
解得x=40.
答:该商品的进价是40元.
(2)根据题意可得,W=x(20-x+1)=21x-x2=-(x-$\frac{21}{2}$)2+$\frac{441}{4}$.
由于商品数为整数及抛物线的对称性可知,当x=10或11时,W有最大值,此时W=110.
即W与x的函数关系式是:W=-(x-$\frac{21}{2}$)2+$\frac{441}{4}$,公司利润的最大值是110元.
(3)由第(2)问可知,当x=11时,取得最大值,当x>11时,二次函数递减,x越大,则利润会越低,
故最低售价为:40+(20-11+1)=50(元).
即应规定最低售价为50元.
点评 本题考查二次函数的应用、二次函数的最值、解一元一次方程,解题的关键能根据题意找出等量关系,列出相应的方程,根据题题可以列出相应的二次函数,把二次函数可以转化为顶点式,然后找出所求问题需要的条件.

练习册系列答案
相关题目
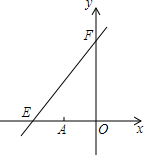 如图,直线y=kx+6与x轴,y轴分别交于点E,F,点E的坐标为(-8,0),点A的坐标是(-6,0).
如图,直线y=kx+6与x轴,y轴分别交于点E,F,点E的坐标为(-8,0),点A的坐标是(-6,0).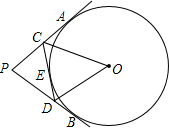 如图,PA,PB切⊙O于点A,B,点E是劣弧$\widehat{AB}$上一点,过E点作⊙O的切线交PA与C,交PB于D,若∠P=80°,∠DOC=50°.
如图,PA,PB切⊙O于点A,B,点E是劣弧$\widehat{AB}$上一点,过E点作⊙O的切线交PA与C,交PB于D,若∠P=80°,∠DOC=50°.