题目内容
12.如图1,已知菱形ABCD的三个顶点A,B,C在矩形EFGH的边上,P是EH上一点,连接HD,BP.(1)当∠APB=∠AHD=∠BAD时,求证:PH=PB+HD;
(2)若EF=10,EH=12,FB=2,△AHD的面积能否等于2?为什么?
(3)如图2,分别连接CP,CH,当∠APB=∠AHD=∠BAD=120°时,△CPH是什么特殊的三角形(不需证明)?
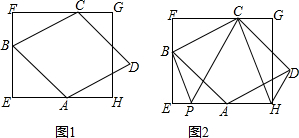
分析 (1)根据菱形的性质得到AB=AD,由等式的性质得到∠PAB=∠ADH,证得△ABP≌△DAH,得到AP=DH,AH=PB,由等量代换得到PH=AP+AH=PB+HD;
(2)如图1过点D作DP⊥EH交EH的延长线于点P,连接AC,构造全等三角形,证得DP=BF=2,由面积公式得到方程,推出边CF>FG,所以△AHD的面积不能等于2;
(3)如图2连接AC,在菱形ABCD中,由菱形的性质得到边角关系,通过三角形全等,得出结论.
解答 解:(1)在菱形ABCD中,
∵AB=AD,
∴∠PAB=190°-∠BAD-∠DAH,
∠ADH=180°-∠AHD-∠DAH,
∴∠PAB=∠ADH,
在△ABP与△DAH中,
$\left\{\begin{array}{l}{∠APB=∠DHA}\\{∠PAB=∠ADH}\\{AB=AD}\end{array}\right.$,
∴△ABP≌△DAH,
∴AP=DH,AH=PB,
∴PH=AP+AH=PB+HD;
(2)如图1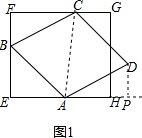 过点D作DP⊥EH交EH的延长线于点P,连接AC,
过点D作DP⊥EH交EH的延长线于点P,连接AC,
∵FG∥EH,
∴∠FCA=∠CAH,
∵BC∥AD,
∴∠BCA=∠DAC,
∴∠FBC=∠DAH,
在△FBC与△DAP中,$\left\{\begin{array}{l}{∠F=∠D=90°}\\{∠FCB=∠DAH}\\{CB=AD}\end{array}\right.$,
∴△FBC≌△DAP,
∴DP=BF=2,
∴S△AHD=$\frac{1}{2}$×2•AH=2,
∴AH=2,AE=10,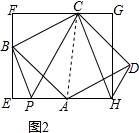
AB2=100+64=164,
∴BC2=164,
∴CF2=164-4=160>FG2=144,
∴△AHD的面积不能等于2;
(3)如图2连接AC,
在菱形ABCD中,
∵∠BAD=120°,
∴∠CBA=∠CAB=∠CAD=60°,
∴BC=AC,
由(1)证得∠PBA=∠DAH,
∴∠CBP=∠CAH,
在△BCP与△CAH中,
$\left\{\begin{array}{l}{BC=AC}\\{∠CBP=∠CAH}\\{BP=AH}\end{array}\right.$,
∴△BCP≌△CAH,
∴PC=CH,∠BPC=∠CHA,
∠CPH=∠CHA=,
∴∠BPC=∠CPA=$\frac{1}{2}BPA$=60°,
∴△PCH是等边三角形.
点评 本题考查了矩形、菱形的性质、全等三角形的判定和性质、勾股定理.解题的关键是作辅助线:过F作FM⊥DC,交DC延长线于M,连接GE,构造全等三角形和内错角.

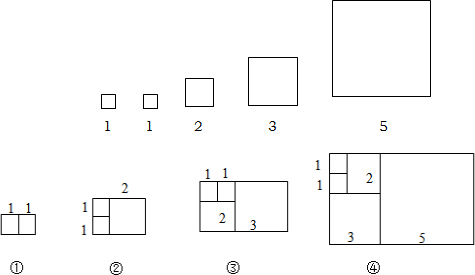
两分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、…相应长方形的周长如表所示:
| 序号 | ① | ② | ③ | ④ | … |
| 周长 | 6 | 10 | x | y | … |
(2)若按此规律继续拼成长方形,则序号为④的长方形周长是26(并写出简要的过程)
(3)以下①、②小题只需选做一小题,若两小题都写,则只按第①小题的解答给分.
①若按此规律拼长方形,已知序号为n的长方形的周长为a,序号为(n+1)的长方形的周长为b,则序号为(n+3)的长方形的周长为a+2b(用含a、b的代数式表示)
②若按此规律继续拼长方形,已知序号为n的长方形的长和宽分别为a、b(其中a<b),则序号为(n+1)的长方形的周长是2a+4b(用含a、b的代数式表示).
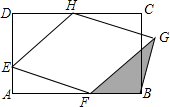 如图,E在矩形ABCD的AD边上,AE=3,ED=5,DC=10,F,H分别在AB,CD上,四边形EFGH是菱形,则△FBG的面积S的取值范围是( )
如图,E在矩形ABCD的AD边上,AE=3,ED=5,DC=10,F,H分别在AB,CD上,四边形EFGH是菱形,则△FBG的面积S的取值范围是( )| A. | 0<S≤15 | B. | 2<S≤12 | C. | 1<S≤15 | D. | 0<S≤12 |
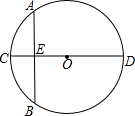 在⊙O上作一条弦AB,再作一条与弦AB垂直的直径CD,CD与AB交于点E,则下列结论中不一定正确是( )
在⊙O上作一条弦AB,再作一条与弦AB垂直的直径CD,CD与AB交于点E,则下列结论中不一定正确是( )| A. | AE=BE | B. | $\widehat{AC}$=$\widehat{BC}$ | C. | CE=EO | D. | $\widehat{AD}$=$\widehat{BD}$ |
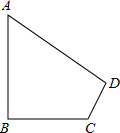 如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求AB的长.
如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求AB的长.