题目内容
17．已知三角形的三边长x、y、z满足（x-z）2=（z-y）（z-x）+（x-z）（2x-z），试判断这个三角形的形状．分析 首先移项，把原式变为（x-z）2-（z-y）（z-x）+（x-z）（2x-z）=0，进一步利用提取公因式法因式分解，探讨得出答案即可．
解答 解：∵（x-z）2=（z-y）（z-x）+（x-z）（2x-z），
∴（x-z）2-（z-y）（z-x）-（x-z）（2x-z）=0，
∴（x-z）（x-z+z-y-2x+z）=0，
∴（x-z）（z-x-y）=0，
∵x、y、z为三角形的三边长，
∴x-z=0，z-x-y≠0，
∴x=z，
∴这个三角形为等腰三角形．
点评 此题考查因式分解的实际运用，掌握提取公因式法是解决问题的关键．
练习册系列答案
全优点练单元计划系列答案
相关题目
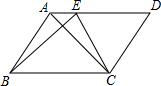已知，如图，?ABCD中，E是边AD上任意一点，求证：S△ABC=S△EBC．
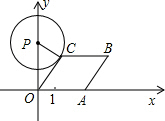如图所示，已知A点从（1，0）点出发，以每秒1个单位长的速度沿着x轴的正方向运动，以O、A为顶点作菱形OABC，使B、C点都在第一象限内，且∠AOC=60°．设经过t秒后，以P（0，3）为圆心，PC为半径的圆恰好与菱形OABC的边所在的直线相切，则t=$\frac{3\sqrt{3}}{2}$-1或$3\sqrt{3}-1$．
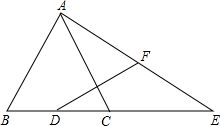如图，已知在△ABC中，AB=AC=2$\sqrt{5}$，sin∠B=$\frac{2\sqrt{5}}{5}$，D为边BC的中点，E为边BC的延长线上一点，且CE=BC．联结AE，F为线段AE的中点．
7．2015年1月1日起，杭州市城区实行全新的阶梯水价，之前为了解某社区居民的用水情况，随机对该社区20户居民进行了调查，下表是这20户居民2014年8月份用水量的调查结果：那么关于这次用水量的调查和数据分析，下列说法错误的是（ ）
| 居民（户） | 1 | 2 | 8 | 6 | 2 | 1 |
| 月用水量（吨） | 4 | 5 | 8 | 12 | 15 | 20 |
| A． | 平均数是10（吨） | B． | 众数是8（吨） | C． | 中位数是10（吨） | D． | 样本容量是20 |