题目内容
3.定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
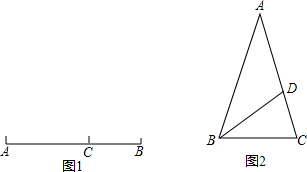
分析 (1)利用等腰三角形的性质和三角形内角和定理可计算出∠ABC=∠C=72°,∠ABD=∠CBD=36°,∠BDC=72°,则可得到AD=BD=BC,然后根据相似三角形的判定方法易得△BDC∽△ABC,利用相似比得到BC2=CD•AC,于是有AD2=CD•AC,则可根据线段黄金分割点的定义得到结论;
(2)设AD=x,则CD=AC-AD=1-x,由(1)的结论得到x2=1-x,然后解方程即可得到AD的长.
解答 (1)证明:∵AB=AC=1,
∴∠ABC=∠C=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-36°)=72°,
∵BD平分∠ABC交AC于点D,
∴∠ABD=∠CBD=$\frac{1}{2}$∠ABC=36°,
∴∠BDC=180°-36°-72°=72°,
∴DA=DB,BD=BC,
∴AD=BD=BC,
易得△BDC∽△ABC,
∴BC:AC=CD:BC,即BC2=CD•AC,
∴AD2=CD•AC,
∴点D是线段AC的黄金分割点;
(2)设AD=x,则CD=AC-AD=1-x,
∵AD2=CD•AC,
∴x2=1-x,解得x1=$\frac{\sqrt{5}-1}{2}$,x2=$\frac{-\sqrt{5}-1}{2}$,
即AD的长为$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.

练习册系列答案
相关题目
15.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
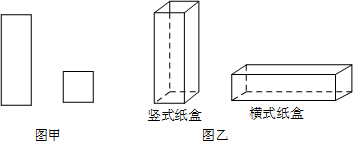
(1)根据题意,完成以下表格:
(2)按两种纸盒的生产个数来分,有哪几种生产方案?
(3)如果做一个竖式纸盒的费用为2元,做一个横式纸盒的费用为1元,如何安排设计方案,使得生产费用最少?

(1)根据题意,完成以下表格:
(2)按两种纸盒的生产个数来分,有哪几种生产方案?
(3)如果做一个竖式纸盒的费用为2元,做一个横式纸盒的费用为1元,如何安排设计方案,使得生产费用最少?
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | 100-x | |
| 正方形纸板(张) | x | 2(100-x) |
| 长方形纸板(张) | 4x | 3(100-x) |
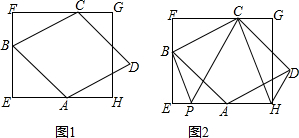
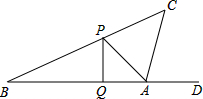 如图,小唐同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处;此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.
如图,小唐同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处;此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.