题目内容
12.以x为自变量的二次函数y=x2-2(b-2)x+b2-1的图象不经过第三象限,则实数b的取值范围是( )| A. | b≥$\frac{5}{4}$ | B. | b≥1或b≤-1 | C. | b≥2 | D. | 1≤b≤2 |
分析 由于二次函数y=x2-2(b-2)x+b2-1的图象不经过第三象限,所以抛物线的顶点在x轴的上方或在x轴的下方经过一、二、四象限,根据二次项系数知道抛物线开口方向向上,由此可以确定抛物线与x轴有无交点,抛物线与y轴的交点的位置,由此即可得出关于b的不等式组,解不等式组即可求解.
解答 解:∵二次函数y=x2-2(b-2)x+b2-1的图象不经过第三象限,
∵二次项系数a=1,
∴抛物线开口方向向上,
当抛物线的顶点在x轴上方时,
则b2-1≥0,△=[2(b-2)]2-4(b2-1)≤0,
解得b≥$\frac{5}{4}$;
当抛物线的顶点在x轴的下方时,
设抛物线与x轴的交点的横坐标分别为x1,x2,
∴x1+x2=2(b-2)>0,b2-1>0,
∴△=[2(b-2)]2-4(b2-1)>0,①
b-2>0,②
b2-1>0,③
由①得b<$\frac{5}{4}$,由②得b>2,
∴此种情况不存在,
∴b≥$\frac{5}{4}$,
故选A.
点评 此题主要考查了二次函数的图象和性质,解题的关键是会根据图象的位置得到关于b的不等式组解决问题.

练习册系列答案
相关题目
20.在反比例函数y=$\frac{1-3k}{x}$的图象上有两点A(x1,y1),B(x2,y2),当0<x1<x2时,有y1>y2,则k的取值范围是( )
| A. | k$>\frac{1}{3}$ | B. | k$<\frac{1}{3}$ | C. | k$≥\frac{1}{3}$ | D. | k$≤\frac{1}{3}$ |
7.已知方程x-2y+3=8,则整式x-2y的值为( )
| A. | 5 | B. | 10 | C. | 12 | D. | 15 |
17.“一方有难,八方支援”,雅安芦山4•20地震后,某单位为一中学捐赠了一批新桌椅,学校组织初一年级200名学生搬桌椅.规定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬一次,最多可搬桌椅(一桌一椅为一套)的套数为( )
| A. | 60 | B. | 70 | C. | 80 | D. | 90 |
4.在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等)现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为( )
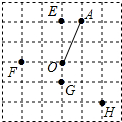

| A. | E、F、G | B. | F、G、H | C. | G、H、E | D. | H、E、F |
2.若二次三项式x2-mx+16是一个完全平方式,则字母m的值是( )
| A. | 4 | B. | -4 | C. | ±4 | D. | ±8 |
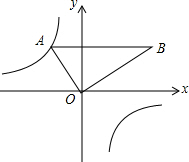 如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.