题目内容
20.在反比例函数y=$\frac{1-3k}{x}$的图象上有两点A(x1,y1),B(x2,y2),当0<x1<x2时,有y1>y2,则k的取值范围是( )| A. | k$>\frac{1}{3}$ | B. | k$<\frac{1}{3}$ | C. | k$≥\frac{1}{3}$ | D. | k$≤\frac{1}{3}$ |
分析 根据反比例函数的单调性结合反比例函数的性质,即可得出关于k的一元一次不等式,解不等式即可得出结论.
解答 解:∵当0<x1<x2时,有y1>y2,
∴该反比例函数在x>0时,y值随x的增大而减小,
∴1-3k>0,
解得:k<$\frac{1}{3}$.
故选B.
点评 本题考查了反比例函数的性质以及解一元一次不等式,解题的关键是找出关于k的一元一次不等式1-3k>0.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数的单调性结合反比例函数性质,得出不等式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.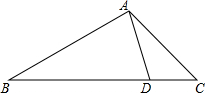 如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
 如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )| A. | 15 | B. | 10 | C. | $\frac{15}{2}$ | D. | 5 |
15.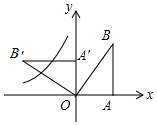 如图,在平面直角坐标系中,Rt△OAB的顶点A、B的坐标分别是(2,0),(2,4),将△OAB绕点O逆时针方向旋转90°,得到△OA′B′,函数y=$\frac{k}{x}$(x<0)的图象过A′B′的中点C,则k的值为( )
如图,在平面直角坐标系中,Rt△OAB的顶点A、B的坐标分别是(2,0),(2,4),将△OAB绕点O逆时针方向旋转90°,得到△OA′B′,函数y=$\frac{k}{x}$(x<0)的图象过A′B′的中点C,则k的值为( )
 如图,在平面直角坐标系中,Rt△OAB的顶点A、B的坐标分别是(2,0),(2,4),将△OAB绕点O逆时针方向旋转90°,得到△OA′B′,函数y=$\frac{k}{x}$(x<0)的图象过A′B′的中点C,则k的值为( )
如图,在平面直角坐标系中,Rt△OAB的顶点A、B的坐标分别是(2,0),(2,4),将△OAB绕点O逆时针方向旋转90°,得到△OA′B′,函数y=$\frac{k}{x}$(x<0)的图象过A′B′的中点C,则k的值为( )| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
12.以x为自变量的二次函数y=x2-2(b-2)x+b2-1的图象不经过第三象限,则实数b的取值范围是( )
| A. | b≥$\frac{5}{4}$ | B. | b≥1或b≤-1 | C. | b≥2 | D. | 1≤b≤2 |
10.已知多项式x2+bx+c分解因式为(x-3)(x+1),则b、c的值为( )
| A. | b=2,c=3 | B. | b=-4,c=3 | C. | b=-2,c=-3 | D. | b=-4,c=-3 |
 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1 A2,…,△PnAn-1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点Pn的坐标是($\sqrt{n}$+$\sqrt{n-1}$,$\sqrt{n}$-$\sqrt{n-1}$);(用含n的代数式表示)
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1 A2,…,△PnAn-1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点Pn的坐标是($\sqrt{n}$+$\sqrt{n-1}$,$\sqrt{n}$-$\sqrt{n-1}$);(用含n的代数式表示) 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是(2n-1,2n-1).
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是(2n-1,2n-1).