题目内容
2.若a、b互为相反数,c、d互为倒数,|m|=3,则$\frac{a+b}{4m}+{m}^{2}-3cd+5m$的值为21或-9.分析 直接利用相反数以及互为倒数和绝对值的性质得出各式的值进而得出答案.
解答 解:∵a、b互为相反数,c、d互为倒数,|m|=3,
∴a+b=0,cd=1,m=±3,
∴$\frac{a+b}{4m}+{m}^{2}-3cd+5m$
=0+9-3±15
=21或-9,
故答案为:21或-9.
点评 此题主要考查了相反数以及互为倒数和绝对值的性质,正确掌握相关定义是解题关键.

练习册系列答案
相关题目
17.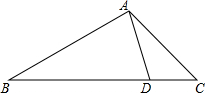 如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
 如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
如图,D是△ABC的边BC上一点,AB=8,AD=4,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )| A. | 15 | B. | 10 | C. | $\frac{15}{2}$ | D. | 5 |
12.以x为自变量的二次函数y=x2-2(b-2)x+b2-1的图象不经过第三象限,则实数b的取值范围是( )
| A. | b≥$\frac{5}{4}$ | B. | b≥1或b≤-1 | C. | b≥2 | D. | 1≤b≤2 |
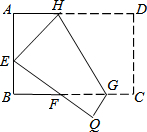 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是8cm.
如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是8cm.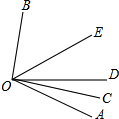 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线. 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1 A2,…,△PnAn-1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点Pn的坐标是($\sqrt{n}$+$\sqrt{n-1}$,$\sqrt{n}$-$\sqrt{n-1}$);(用含n的代数式表示)
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1 A2,…,△PnAn-1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),则点Pn的坐标是($\sqrt{n}$+$\sqrt{n-1}$,$\sqrt{n}$-$\sqrt{n-1}$);(用含n的代数式表示)