题目内容
16.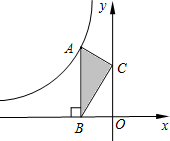 如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
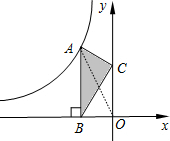
分析 连结OA,如图,利用三角形面积公式得到S△OAB=S△CAB=3,再根据反比例函数的比例系数k的几何意义得到$\frac{1}{2}$|k|=3,然后去绝对值即可得到满足条件的k的值.
解答 解:连结OA,如图,
∵ AB⊥x轴,
AB⊥x轴,
∴OC∥AB,
∴S△OAB=S△CAB=3,
而S△OAB=$\frac{1}{2}$|k|,
∴$\frac{1}{2}$|k|=3,
∵k<0,
∴k=-6.
故选D.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
相关题目
6.下列计算中,正确的是( )
| A. | (a2b)3=a6b | B. | a2•a3=a6 | C. | a6÷a3=a3 | D. | ${(\frac{a}{b})^3}=\frac{a^3}{b}$ |
11.某市3月下旬抽样六天的最高气温如下(单位℃):18,19,20,21,19,23,对这组数据下列说法错误的是( )
| A. | 平均数是20 | B. | 众数是19 | C. | 中位数是21 | D. | 都不正确 |
8.计算a2÷a3的结果是( )
| A. | a-1 | B. | a | C. | a5 | D. | a6 |
 如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为35°.
如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为35°. 如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?