题目内容
1.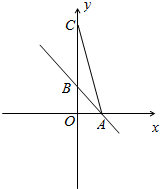 如图,一次函数y=-x+1的图象与x轴,y轴分别交于点A,B,点C在y轴的正半轴上,且OC=3.在直线AB上有一点P,若满足∠CPB>∠ACB,则点P横坐标x的取值范围是-4<x<2且x≠0.
如图,一次函数y=-x+1的图象与x轴,y轴分别交于点A,B,点C在y轴的正半轴上,且OC=3.在直线AB上有一点P,若满足∠CPB>∠ACB,则点P横坐标x的取值范围是-4<x<2且x≠0.
分析 首先利用一次函数解析式得出AO,BO的长,再利用勾股定理得出AC,AB的长,再利用相似三角形的判定与性质得出即可.
解答 解:如图所示:过点P1作P1E⊥x轴于点E,
∵一次函数y=-x+1的图象与x轴,y轴分别交于点A,B,点C在y轴的正半轴上,且OC=3,
∴AO=BO=1,则BC=2,AC=$\sqrt{10}$,AB=$\sqrt{2}$,
当∠CP1B=∠ACB时,
又∵∠CAB=∠CAP1,
∴△CAB∽△P1AC,
∴$\frac{AC}{A{P}_{1}}$=$\frac{AB}{AC}$,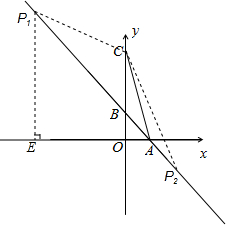
则$\frac{\sqrt{10}}{A{P}_{1}}$=$\frac{\sqrt{2}}{\sqrt{10}}$,
解得:AP1=5$\sqrt{2}$,
则AE=P1E=5,
故P1(-4,5),
当∠CPB>∠ACB时,则点P横坐标x满足:-4<x,
同理可得:当∠CP2B=∠ACB时,
又∵∠ABC=∠P2BC,
∴△CAB∽△P2CB,
∴$\frac{AB}{BC}$=$\frac{BC}{B{P}_{2}}$,
则$\frac{\sqrt{2}}{2}$=$\frac{2}{B{P}_{2}}$,
解得:BP2=2$\sqrt{2}$,
可得P2(2,-1),
故当∠CPB>∠ACB时,则点P横坐标x满足:2>x,当x=1时,A,P点重合,不合题意舍去.
综上所述:-4<x<2且x≠0.
故答案为:-4<x<2且x≠0.
点评 此题主要考查了一次函数综合以及相似三角形的判定与性质,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
3.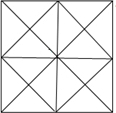 对于给定的单位正方形,若将其两条对角线以及每两条边的中点连线作出,便得到如图,则图中互为相似的三角形“对子”数为( )
对于给定的单位正方形,若将其两条对角线以及每两条边的中点连线作出,便得到如图,则图中互为相似的三角形“对子”数为( )
 对于给定的单位正方形,若将其两条对角线以及每两条边的中点连线作出,便得到如图,则图中互为相似的三角形“对子”数为( )
对于给定的单位正方形,若将其两条对角线以及每两条边的中点连线作出,便得到如图,则图中互为相似的三角形“对子”数为( )| A. | 44对 | B. | 552对 | C. | 946对 | D. | 1892对 |
11.关于x的方程x-2=m的解为正实数,则m的取值范围是( )
| A. | m≥2 | B. | m≤2 | C. | m>-2 | D. | m<2 |
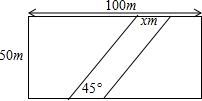 如图,在草坪中间修一条小路,小路的横向宽为x m,设开辟道路后草地的实际面积为y m2.
如图,在草坪中间修一条小路,小路的横向宽为x m,设开辟道路后草地的实际面积为y m2.