题目内容
14. 如图,直线OC、BC的函数关系是分别是y1=x和y2=-2x+6,直线BC与x轴交于点B,直线BA与直线OC相交于点A,求:
如图,直线OC、BC的函数关系是分别是y1=x和y2=-2x+6,直线BC与x轴交于点B,直线BA与直线OC相交于点A,求:(1)求点C的坐标.
(2)当直线BA平分△BOC的面积时,求点A的坐标.
分析 (1)联立两函数关系式解二元一次方程组即可得到点C的坐标;
(2)根据三角形的中线把三角形分成面积相等的两部分可知点A是OC的中点,然后根据点C的坐标写出即可.
解答 解:(1)联立$\left\{\begin{array}{l}{y=x}\\{y=-2x+6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
所以,点C的坐标为(2,2);
(2)∵直线BA平分△BOC的面积,
∴BA是△BOC的中线,
∴点A是OC的中点,
∴点A的坐标为(1,1).
点评 本题考查了两条直线相交或平行问题,主要利用了联立两函数解析式求交点的方法,三角形的中线把三角形分成面积相等的两部分.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
2. 如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则DF的长是( )
如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则DF的长是( )
 如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则DF的长是( )
如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则DF的长是( )| A. | 3 | B. | 4 | C. | 4.8 | D. | 5 |
19.在学校举行的“舞动育才”班级舞蹈大赛中,八年级某班的得分情况如下:92,88,95,93,96,95,94.这组数据的众数和中位数分别是( )
| A. | 94,94 | B. | 95,95 | C. | 94,95 | D. | 95,94 |
 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:
二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法: 如图,从给出的四个条件:
如图,从给出的四个条件: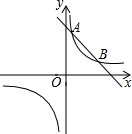 如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数y=-x+3的图象交于A(1,m),B(n,1)两点.
如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数y=-x+3的图象交于A(1,m),B(n,1)两点.