题目内容
3.随着人民生活水平的不断提高,某社区家庭轿车拥有量逐年增加.据统计,一居民小区2009年底拥有家庭轿车100辆,2011年底家庭轿车拥有量达到144辆.(1)若该小区2009年底到2012年底家庭轿车拥有量的年平均增长率相同,求该小区到2012年底家庭轿车将达到多少辆(结果取整数).
(2)为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个,试写出所有可能的方案.
分析 (1)增长率的问题,用解增长率问题的模型解答;
(2)根据两种车位数量是未知数,建立等式和不等式两种关系,而车位数为整数,变无数解为有限解.方案也就出来了.
解答 解:(1)设该小区2009年底到2012年底家庭轿车拥有量的年平均增长率为x,
根据题意得 100(1+x)2=144,
解之得x1=0.2,x2=-2.2(不合题意,舍去),
∴144(1+0.2)=172.8≈173;
答:该小区到2012年底家庭轿车将达到173辆;
(2)设该小区建露天车位x个,室内车位y个,
由题意得$\left\{\begin{array}{l}1000x+5000y=150000\\ 2y≤x≤2.5y\end{array}\right.$,
解之得$20≤y≤\frac{150}{7}$,
∵y取整数,
∴y=20或21,
当y=20时,x=50,当y=21时,x=45,
答:该小区最多可建露天车位50个,最多可建室内车位21个;
当建露天车位50个时室内车位为20个,
当建露天车位45个时室内车位为21个.
点评 本题考查一元二次方程及一元一次不等式组的应用,关键是先求出增长率,再求出2012年的轿车量,然后根据室内车位和露天车位的数量关系列出不等式组求解.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
13.下列命题是假命题的是( )
| A. | 两条边和它们的夹角对应相等的两个三角形全等 | |
| B. | 两边分别相等且其中一组等边的对角相等的两个三角形全等 | |
| C. | 平面内,经过一点有一条直线并且只有一条直线与已知直线垂直 | |
| D. | 三角形的一条中线能将三角形分成面积相等的两个部分 |
11.用配方法解关于x的一元二次方程x2-2x-8=0,配方后的方程可以是( )
| A. | (x+1)2=9 | B. | (x-1)2=9 | C. | (x+1)2=8 | D. | (x-1)2=8 |
15. 一只茶壶如图所示放置,从正面看到的几何体的形状图是( )
一只茶壶如图所示放置,从正面看到的几何体的形状图是( )
 一只茶壶如图所示放置,从正面看到的几何体的形状图是( )
一只茶壶如图所示放置,从正面看到的几何体的形状图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,直线OC、BC的函数关系是分别是y1=x和y2=-2x+6,直线BC与x轴交于点B,直线BA与直线OC相交于点A,求:
如图,直线OC、BC的函数关系是分别是y1=x和y2=-2x+6,直线BC与x轴交于点B,直线BA与直线OC相交于点A,求: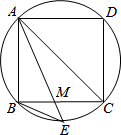 如图,在边长为4cm的圆内接正方形ABCD中,AC是对角线,M为边BC的中点,延长AM交圆于点E.
如图,在边长为4cm的圆内接正方形ABCD中,AC是对角线,M为边BC的中点,延长AM交圆于点E.