题目内容
6.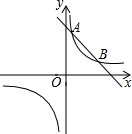 如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数y=-x+3的图象交于A(1,m),B(n,1)两点.
如图,反比例函数y=$\frac{k}{x}$(k>0)的图象与一次函数y=-x+3的图象交于A(1,m),B(n,1)两点.(1)求这个反比例函数的表达式;
(2)请直接写出使一次函数值小于反比例函数值的x的取值范围.
分析 (1)把A和B的坐标代入反比例函数解析式求得m、n的值,然后利用待定系数法求得反比例函数的解析式.
(2)根据A、B的横坐标结合图象即可得出答案.
解答 解:(1)把A(1,m)代入y=-x+3的得:m=2,则A的坐标是(1,2),
把B(n,1)代入y=-x+3得:n=2,则B的坐标是(2,1).
解得:k=2×1=2,
则反比例函数的解析式是y=$\frac{2}{x}$;
(2)∵A(1,2),B(2,1),
观察图象可知,当0<x<1或x>2时,一次函数的图象在反比例函数图象的下方,
故一次函数的值小于反比例函数的值的x的取值范围是0<x<1或x>2.
点评 本题考查了待定系数法求函数的解析式、三角形的面积的计算以及函数的图象的应用,正确求得直线的解析式和数形结合思想的应用是解题的关键.

练习册系列答案
相关题目
11.用配方法解关于x的一元二次方程x2-2x-8=0,配方后的方程可以是( )
| A. | (x+1)2=9 | B. | (x-1)2=9 | C. | (x+1)2=8 | D. | (x-1)2=8 |
15. 一只茶壶如图所示放置,从正面看到的几何体的形状图是( )
一只茶壶如图所示放置,从正面看到的几何体的形状图是( )
 一只茶壶如图所示放置,从正面看到的几何体的形状图是( )
一只茶壶如图所示放置,从正面看到的几何体的形状图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,一艘货轮以20海里/时的速度在海面上航行,当它行驶到A处时,发现它的东北方向有一灯塔B.货轮继续向北航行1小时后到达C处,发现灯塔B在它北偏东75°方向,那么此时货轮与灯塔B的距离为20$\sqrt{2}$海里(结果不取近似值).
如图,一艘货轮以20海里/时的速度在海面上航行,当它行驶到A处时,发现它的东北方向有一灯塔B.货轮继续向北航行1小时后到达C处,发现灯塔B在它北偏东75°方向,那么此时货轮与灯塔B的距离为20$\sqrt{2}$海里(结果不取近似值). 如图,直线OC、BC的函数关系是分别是y1=x和y2=-2x+6,直线BC与x轴交于点B,直线BA与直线OC相交于点A,求:
如图,直线OC、BC的函数关系是分别是y1=x和y2=-2x+6,直线BC与x轴交于点B,直线BA与直线OC相交于点A,求: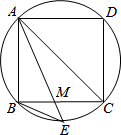 如图,在边长为4cm的圆内接正方形ABCD中,AC是对角线,M为边BC的中点,延长AM交圆于点E.
如图,在边长为4cm的圆内接正方形ABCD中,AC是对角线,M为边BC的中点,延长AM交圆于点E. 如图,已知AB∥CD,∠A=∠C,试说明∠B=∠F.
如图,已知AB∥CD,∠A=∠C,试说明∠B=∠F.