题目内容
16. 如图.已知直线AB∥CD,∠DCF=110°,∠A=50°,则∠E等于60°.
如图.已知直线AB∥CD,∠DCF=110°,∠A=50°,则∠E等于60°.
分析 由AB∥CD利用“两直线平行,同位角相等”即可得出∠BFE=∠DCF=110°,再根据外角的性质即可得出结论.
解答 解:∵AB∥CD,∠DCF=110°,
∴∠BFE=∠DCF=110°.
又∵∠BFE=∠A+∠E,∠A=50°,
∴∠E=∠BFE-∠A=110°-50°=60°.
故答案为:60°.
点评 本题考查了平行线的性质以及三角形外角的性质,解题的关键是得出∠BFE=110°.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等(或互补)的角是关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
6.在?ABCD中,若∠A+∠C=200°,则∠B的大小为( )
| A. | 160° | B. | 100° | C. | 80° | D. | 60° |
7. 已知一次函数y=ax+c的图象如图所示,那么一元二次方程ax2+bx+c=0的根的情况是( )
已知一次函数y=ax+c的图象如图所示,那么一元二次方程ax2+bx+c=0的根的情况是( )
 已知一次函数y=ax+c的图象如图所示,那么一元二次方程ax2+bx+c=0的根的情况是( )
已知一次函数y=ax+c的图象如图所示,那么一元二次方程ax2+bx+c=0的根的情况是( )| A. | 方程有两个不相等的实数根 | B. | 方程有两个相等的实数根 | ||
| C. | 方程没有实数根 | D. | 无法判断 |
11. 如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )
如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )
 如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )
如图,直线AB∥CD,∠C=115°,∠A=25°,则∠E的度数为( )| A. | 100° | B. | 90° | C. | 80° | D. | 70° |
1.我国最大的领海是南海,总面积有3 500 000平方公里,将数3 500 000用科学记数法表示应为( )
| A. | 3.5×106 | B. | 3.5×107 | C. | 35×105 | D. | 0.35×108 |
8.对于方程y2+5y-1=0,下列说法正确的是( )
| A. | 方程无实数根 | B. | 方程有两个相等的实数根 | ||
| C. | 方程有两个不相等的实数根 | D. | 方程的根无法确定 |
3. 如图,在正方形ABCD中,点E,F分别在AB,AD上,且BE=AF,连接CE,BF相交于点G,则下列结论不正确的是( )
如图,在正方形ABCD中,点E,F分别在AB,AD上,且BE=AF,连接CE,BF相交于点G,则下列结论不正确的是( )
 如图,在正方形ABCD中,点E,F分别在AB,AD上,且BE=AF,连接CE,BF相交于点G,则下列结论不正确的是( )
如图,在正方形ABCD中,点E,F分别在AB,AD上,且BE=AF,连接CE,BF相交于点G,则下列结论不正确的是( )| A. | BF=CE | B. | ∠AFB=∠ECD | C. | BF⊥CE | D. | ∠AFB+∠BEC=90° |
 “瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”的图案中,是轴对称图形的为( )
“瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”的图案中,是轴对称图形的为( )



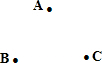 如图,点A,B,C不在同一直线线上.请利用圆规和直尺按下列要求作图(保留作图痕迹,不写作法).
如图,点A,B,C不在同一直线线上.请利用圆规和直尺按下列要求作图(保留作图痕迹,不写作法).