题目内容
2.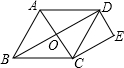 已知:如图,O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,DE、CE交于点E.
已知:如图,O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,DE、CE交于点E.(1)猜想:四边形CEDO是什么特殊的四边形?
(2)试证明你的猜想.
分析 (1)猜想:四边形CEDO是矩形;
(2)根据平行四边形的判定推出四边形是平行四边形,根据菱形性质求出∠DOC=90°,根据矩形的判定推出即可;
解答 (1)解:猜想:四边形CEDO是矩形.
(2)证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴四边形OCED是矩形.
点评 本题考查了矩形的判定,平行四边形的判定,菱形的性质的应用,注意:有一个角是直角的平行四边形是矩形.

练习册系列答案
相关题目
12.在下列所给出坐标的点中,在第三象限的是( )
| A. | (2,3) | B. | (-2,-3) | C. | (-2,3) | D. | (2,-3) |
10.解不等式组$\left\{\begin{array}{l}{x+2>0}\\{2(x-1)+3≥3x}\end{array}\right.$并判断x=-$\sqrt{3}$是否为该不等式组的解.
14.下列结论正确的是( )
| A. | 不相交的两条直线叫做平行线 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 垂直于同一直线的两条直线互相平行 | |
| D. | 平行于同一直线的两条直线互相平行 |
4.化简$\sqrt{4{x}^{2}-4x+1}$-($\sqrt{(1-3x)}$)2 得( )
| A. | x | B. | 5x-2 | C. | -x | D. | -5x+2 |