题目内容
3．
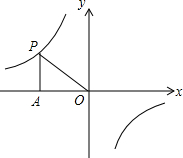如图，已知点P是双曲线y=$\frac{k}{x}$（k≠0）上一点，过点P作PA⊥x轴于点A，且S△PAO=2，则该双曲线的解析式为（ ）| A． | y=-$\frac{4}{x}$ | B． | y=-$\frac{2}{x}$ | C． | y=$\frac{4}{x}$ | D． | y=$\frac{2}{x}$ |
分析 先判断出k的符号，再由反比例函数系数k的几何意义即可得出结论．
解答 解：∵反比例函数的图象在二四象限，
∴k＜0．
∵PA⊥x轴于点A，且S△PAO=2，
∴k=-4，
∴反比例函数的解析式为y=-$\frac{4}{x}$．
故选A．
点评 本题考查的是用待定系数法求反比例函数的解析式，熟知反比例函数系数k的几何意义是解答此题的关键．
练习册系列答案
相关题目
13．对于数据：6，3，4，7，6，0，9，下列判断中正确的是（ ）
| A． | 这组数据的平均数是6，中位数是6 | B． | 这组数据的平均数是5，中位数是6 | ||
| C． | 这组数据的平均数是6，中位数是7 | D． | 这组数据的平均数是5，中位数是7 |
11．
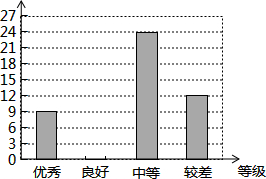为进一步加强学习贯彻2015年新修订的《中小学生守则》，某校组织全校学生参加安溪县中小学“学守则•促文明•行规范”校园猜谜比赛，将比赛成绩分为“优秀、良好、中等、较差”四个等级．现从中随机抽取该校部分学生的比赛成绩进行统计分析，并制成了如下的统计图表：
根据图表信息，回答下列问题：
（1）本次抽查的学生共有60名；
（2）统计表中所表示的数a=15，b=20%，并将条形统计图补充完整；
（3）已知该校共有1800名学生参加比赛，请你估计比赛成绩达到“良好”或“优秀”等级的人数约是多少？
为进一步加强学习贯彻2015年新修订的《中小学生守则》，某校组织全校学生参加安溪县中小学“学守则•促文明•行规范”校园猜谜比赛，将比赛成绩分为“优秀、良好、中等、较差”四个等级．现从中随机抽取该校部分学生的比赛成绩进行统计分析，并制成了如下的统计图表：| 比赛成绩等级 | 人数 | 百分比 |
| 较差 | 12 | b |
| 中等 | 24 | c |
| 良好 | a | 25% |
| 优秀 | 9 | 15% |
（1）本次抽查的学生共有60名；
（2）统计表中所表示的数a=15，b=20%，并将条形统计图补充完整；
（3）已知该校共有1800名学生参加比赛，请你估计比赛成绩达到“良好”或“优秀”等级的人数约是多少？
如图，AD∥BE∥CF，直线l1，l2与三条平行线分别交于点A，B，C和点D，E，F．若AC=3，BC=2，DE=1.5，则DF的长为4.5．
8．下列各式正确的是（ ）
| A． | x2+x3=x5 | B． | x3•x2=2x5 | C． | x5÷x3=x2 | D． | （x5）2=x7 |
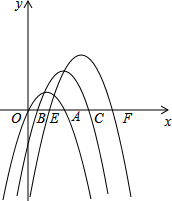已知，如图，将抛物线y1=-（x-1）2+1，y2=-（x-2）2+2，y3=-（x-3）2+3，…，yn=-（x-n）2+n（n为正整数）称为“系列抛物线”，其分别与x轴交于点O，A，B，C，E，F，…．
12．在一个凸n边形的纸板上切下一个三角形后，剩下的一个内角和为1080°的多边形，则n的值为（ ）
| A． | 7 | B． | 8 | C． | 9 | D． | 以上都有可能 |