题目内容
13．解不等式组$\left\{\begin{array}{l}x-3（x-2）≤4\\ \frac{1+2x}{3}＞x-1\end{array}\right.$，并把它的解集在数轴上表示出来．分析 首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．
解答 解：$\left\{\begin{array}{l}{x-3（x-2）≤4…①}\\{\frac{1+2x}{3}＞x-1…②}\end{array}\right.$，
由①得：x≥1，由②得x＜4，
则不等式组的解集为：1≤x＜4．
点评 本题考查了不等式组的解法，把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
3．
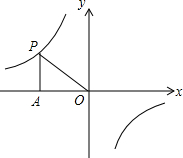如图，已知点P是双曲线y=$\frac{k}{x}$（k≠0）上一点，过点P作PA⊥x轴于点A，且S△PAO=2，则该双曲线的解析式为（ ）
如图，已知点P是双曲线y=$\frac{k}{x}$（k≠0）上一点，过点P作PA⊥x轴于点A，且S△PAO=2，则该双曲线的解析式为（ ）| A． | y=-$\frac{4}{x}$ | B． | y=-$\frac{2}{x}$ | C． | y=$\frac{4}{x}$ | D． | y=$\frac{2}{x}$ |
4．在|-3|，30，3-2，$\sqrt{3}$这四个数中，最大的数是（ ）
| A． | |-3| | B． | 30 | C． | 3-2 | D． | $\sqrt{3}$ |
如图，已知一次函数y=kx+b的图象经过点A（2，1），且y的值随着x的值增大而减小，当函数值y≥1时，那么x的取值范围是x≤2．
18．
一次函数y=kx+b（k≠0，k与b都是常数）图象如图示，当y＜2时，变量x的取值范围是（ ）
一次函数y=kx+b（k≠0，k与b都是常数）图象如图示，当y＜2时，变量x的取值范围是（ ）| A． | x＞0 | B． | x＜0 | C． | x＜2 | D． | x＞2 |
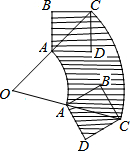如图所示，正方形ABCD对角线AC所在直线上有一点O，OA=AC=2，将正方形绕O点顺时针旋转60°，在旋转过程中，正方形扫过的面积是2π+2．