题目内容
 点A、B、C在平面直角坐标系中的位置如右图,按下列要求回答问题:
点A、B、C在平面直角坐标系中的位置如右图,按下列要求回答问题:(1)用线段将点A、B、C连接成△ABC并写出点A、B、C三点的坐标;
(2)将△ABC先向下平移三个单位,再向左平移五个单位得△A1B1C1画出整个平移过程并求点A1、B1、C1三点坐标;
(3)求S△A1B1C1.
考点:作图-平移变换
专题:作图题
分析:(1)根据平面直角坐标系写出各点的坐标即可;
(2)根据网格结构找出点A、B、C平移后的对应点A1、B1、C1的位置,然后顺次连接即可;
(3)利用△A1B1C1所在的矩形的面积减去四周三个直角三角形的面积,列式计算即可得解.
(2)根据网格结构找出点A、B、C平移后的对应点A1、B1、C1的位置,然后顺次连接即可;
(3)利用△A1B1C1所在的矩形的面积减去四周三个直角三角形的面积,列式计算即可得解.
解答: 解:(1)A(2,3),B(1,1),C(5,2);
解:(1)A(2,3),B(1,1),C(5,2);
(2)△A1B1C1如图所示,A1(-3,0),B1(-4,-2),C1(0,-1);
(3)S△A1B1C1=4×2-
×1×2-
×1×4-
×1×3
=8-1-2-1.5
=8-4.5
=3.5.
 解:(1)A(2,3),B(1,1),C(5,2);
解:(1)A(2,3),B(1,1),C(5,2);(2)△A1B1C1如图所示,A1(-3,0),B1(-4,-2),C1(0,-1);
(3)S△A1B1C1=4×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=8-1-2-1.5
=8-4.5
=3.5.
点评:本题考查了利用平移变换作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
在代数式
,-
,
-y2,
,
中,分式的个数有( )
| x |
| 3x+1 |
| x2+1 |
| 2 |
| x |
| 3 |
| 3a-b |
| a+2 |
| x+1 |
| x-1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
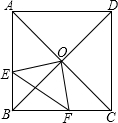 在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,
在正方形ABCD中,O是对角线的交点,过O作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3, 如图,直线y=-
如图,直线y=-