题目内容
1. 如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则Cn的坐标是( )
如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则Cn的坐标是( )| A. | (-$\sqrt{3}$×4n,4n) | B. | (-$\sqrt{3}$×4n-1,4n-1) | C. | (-$\sqrt{3}$×4n-1,4n) | D. | (-$\sqrt{3}$×4n,4n-1) |
分析 先求出直线l的解析式为y=$\frac{\sqrt{3}}{3}$x,设B点坐标为(x,1),根据直线l经过点B,求出B点坐标为($\sqrt{3}$,1),解Rt△A1AB,得出AA1=3,OA1=4,由平行四边形的性质得出A1C1=AB=$\sqrt{3}$,则C1点的坐标为(-$\sqrt{3}$,4),即(-$\sqrt{3}$×40,41);根据直线l经过点B1,求出B1点坐标为(4$\sqrt{3}$,4),解Rt△A2A1B1,得出A1A2=12,OA2=16,由平行四边形的性质得出A2C2=A1B1=4$\sqrt{3}$,则C2点的坐标为(-4$\sqrt{3}$,16),即(-$\sqrt{3}$×41,42);同理,可得C3点的坐标为(-16$\sqrt{3}$,64),即(-$\sqrt{3}$×42,43);进而得出规律,求得Cn的坐标是(-$\sqrt{3}$×4n-1,4n).
解答  解:∵直线l经过原点,且与y轴正半轴所夹的锐角为60°,
解:∵直线l经过原点,且与y轴正半轴所夹的锐角为60°,
∴直线l的解析式为y=$\frac{\sqrt{3}}{3}$x.
∵AB⊥y轴,点A(0,1),
∴可设B点坐标为(x,1),
将B(x,1)代入y=$\frac{\sqrt{3}}{3}$x,得1=$\frac{\sqrt{3}}{3}$x,解得x=$\sqrt{3}$,
∴B点坐标为($\sqrt{3}$,1),AB=$\sqrt{3}$.在Rt△A1AB中,∠AA1B=90°-60°=30°,∠A1AB=90°,
∴AA1=$\sqrt{3}$AB=3,OA1=OA+AA1=1+3=4,
∵?ABA1C1中,A1C1=AB=$\sqrt{3}$,
∴C1点的坐标为(-$\sqrt{3}$,4),即(-$\sqrt{3}$×40,41);
由$\frac{\sqrt{3}}{3}$x=4,解得x=4$\sqrt{3}$,
∴B1点坐标为(4$\sqrt{3}$,4),A1B1=4$\sqrt{3}$.
在Rt△A2A1B1中,∠A1A2B1=30°,∠A2A1B1=90°,
∴A1A2=$\sqrt{3}$A1B1=12,OA2=OA1+A1A2=4+12=16,
∵?A1B1A2C2中,A2C2=A1B1=4$\sqrt{3}$,
∴C2点的坐标为(-4$\sqrt{3}$,16),即(-$\sqrt{3}$×41,42);
同理,可得C3点的坐标为(-16$\sqrt{3}$,64),即(-$\sqrt{3}$×42,43);
以此类推,则Cn的坐标是(-$\sqrt{3}$×4n-1,4n).
故选C.
点评 本题考查了平行四边形的性质,解直角三角形以及一次函数的综合应用,先分别求出C1、C2、C3点的坐标,从而发现规律是解题的关键.

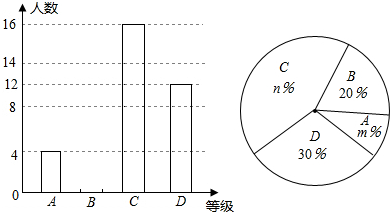
| A. | 参加演讲比赛学生共40人 | |
| B. | 扇形统计图中m=10,n=40 | |
| C. | 学校欲从获A等级的学生中随机选取2人参加市级比赛,选中A等级的小明的概率为$\frac{1}{2}$ | |
| D. | C等级所对应的圆心角为120度 |



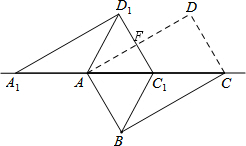 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.