题目内容
16.“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1-(x-a)(x-b)=0的两根,且a<b,则a、b、m、n的大小关系是m<a<b<n.分析 依题意画出函数y=(x-a)(x-b)图象草图,根据二次函数的增减性求解.
解答 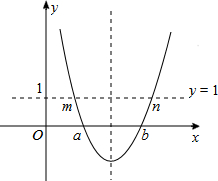 解:依题意,画出函数y=(x-a)(x-b)的图象,如图所示.
解:依题意,画出函数y=(x-a)(x-b)的图象,如图所示.
函数图象为抛物线,开口向上,与x轴两个交点的横坐标分别为a,b(a<b).
方程1-(x-a)(x-b)=0
转化为(x-a)(x-b)=1,
方程的两根是抛物线y=(x-a)(x-b)与直线y=1的两个交点.
由m<n,可知对称轴左侧交点横坐标为m,右侧为n.
由抛物线开口向上,则在对称轴左侧,y随x增大而减少,则有m<a;在对称轴右侧,y随x增大而增大,
则有b<n.
综上所述,可知m<a<b<n.
故答案为:m<a<b<n.
点评 本题考查了二次函数与一元二次方程的关系,考查了数形结合的数学思想.解题时,画出函数草图,由函数图象直观形象地得出结论,避免了繁琐复杂的计算.

练习册系列答案
相关题目
4.下列四句话的文字有三句具有对称规律,其中没有这种规律的一句是( )
| A. | 有志者事竟成 | B. | 上海自来水来自上海 | ||
| C. | 清水池里池水清 | D. | 蜜蜂酿蜂蜜 |
11.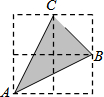 如图,在2×2正方形网格中,以格点为顶点的△ABC的面积等于$\frac{3}{2}$,则sin∠CAB=( )
如图,在2×2正方形网格中,以格点为顶点的△ABC的面积等于$\frac{3}{2}$,则sin∠CAB=( )
 如图,在2×2正方形网格中,以格点为顶点的△ABC的面积等于$\frac{3}{2}$,则sin∠CAB=( )
如图,在2×2正方形网格中,以格点为顶点的△ABC的面积等于$\frac{3}{2}$,则sin∠CAB=( )| A. | $\frac{3}{2}$$\sqrt{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{3}{10}$ |
1. 如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则Cn的坐标是( )
如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则Cn的坐标是( )
 如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则Cn的坐标是( )
如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则Cn的坐标是( )| A. | (-$\sqrt{3}$×4n,4n) | B. | (-$\sqrt{3}$×4n-1,4n-1) | C. | (-$\sqrt{3}$×4n-1,4n) | D. | (-$\sqrt{3}$×4n,4n-1) |
5. 如图,AB为⊙O的直径,P为AB延长线上一点,PT切⊙O于T,若PT=6,PB=2,则⊙O的直径为( )
如图,AB为⊙O的直径,P为AB延长线上一点,PT切⊙O于T,若PT=6,PB=2,则⊙O的直径为( )
 如图,AB为⊙O的直径,P为AB延长线上一点,PT切⊙O于T,若PT=6,PB=2,则⊙O的直径为( )
如图,AB为⊙O的直径,P为AB延长线上一点,PT切⊙O于T,若PT=6,PB=2,则⊙O的直径为( )| A. | 8 | B. | 10 | C. | 16 | D. | 18 |
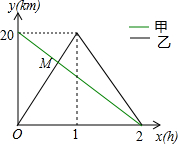 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: