题目内容
20.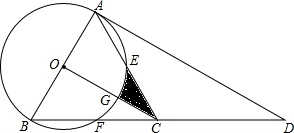 如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F
如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F(1)求证:AD是⊙O的切线;
(2)连接OC,交⊙O于点G,若AB=4,求线段CE、CG与$\widehat{GE}$围成的阴影部分的面积S.
分析 (1)求出∠DAC=30°,即可求出∠DAB=90°,根据切线的判定推出即可;
(2)连接OE,分别求出△AOE、△AOC,扇形OEG的面积,即可求出答案.
解答 (1)证明:∵△ABC为等边三角形,
∴AC=BC,
又∵AC=CD,
∴AC=BC=CD,
∴△ABD为直角三角形,
∴AB⊥AD,
∵AB为直径,
∴AD是⊙O的切线;
(2)解:连接OE,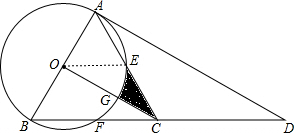
∵OA=OE,∠BAC=60°,
∴△OAE是等边三角形,
∴∠AOE=60°,
∵CB=BA,OA=OB,
∴CO⊥AB,
∴∠AOC=90°,
∴∠EOC=30°,
∵△ABC是边长为4的等边三角形,
∴AO=2,由勾股定理得:OC=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
同理等边三角形AOE边AO上高是$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
S阴影=S△AOC-S等边△AOE-S扇形EOG=$\frac{1}{2}•2•2\sqrt{3}-\frac{1}{2}•2•\sqrt{3}-\frac{30•π•{2}^{2}}{360}$=$\sqrt{3}-\frac{π}{3}$.
点评 本题考查了等边三角形的性质和判定,勾股定理,三角形面积,扇形的面积,切线的判定的应用,能综合运用定理进行推理和计算是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.方程$\frac{1}{1-x}+\frac{x}{x-1}$=-1的解是( )
| A. | x=2 | B. | x=1 | C. | x=0 | D. | 无实数解 |
15.下列图案中既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.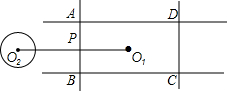 如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
 如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )| A. | 18次 | B. | 12次 | C. | 8次 | D. | 4次 |
9.若菱形的周长为24cm,一个内角为60°,则菱形较短的一条对角线为( )
| A. | 9cm | B. | 8cm | C. | 7cm | D. | 6cm |
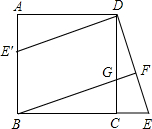 如图,在正方形ABCD中,G是CD上一点,延长BC到点E,CE=CG,连接BG并延长交DE于F.
如图,在正方形ABCD中,G是CD上一点,延长BC到点E,CE=CG,连接BG并延长交DE于F.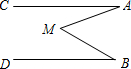 如图,AC∥DB,∠A=20°,∠B=30°,那么∠AMB=50°.
如图,AC∥DB,∠A=20°,∠B=30°,那么∠AMB=50°.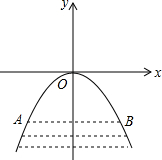 某涵洞是抛物线形,它的截面如图所示,现测得水面宽AB=1.6米,涵洞顶点O到水面的距离为2.4米,建立如图所示的直角坐标系.
某涵洞是抛物线形,它的截面如图所示,现测得水面宽AB=1.6米,涵洞顶点O到水面的距离为2.4米,建立如图所示的直角坐标系.