题目内容
6.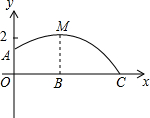 如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M,距地面4米高,球落地为C点.
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M,距地面4米高,球落地为C点.(1)求足球开始飞出到第一次落地时,该抛物线的解析式;
(2)足球第一次落地点C距守门员多少米?
分析 (1)以O为原点,直线OA为y轴,直线OB为x轴建直角坐标系,得出抛物线的顶点是(6,4),利用顶点式求出解析式即可;
(2)利用令y=0,则-$\frac{1}{12}$x2+x+1=0,求出图象与x轴交点坐标即可得出答案.
解答 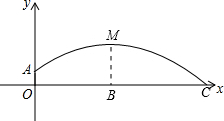 解:(1)以O为原点,直线OA为y轴,直线OB为x轴建直角坐标系.
解:(1)以O为原点,直线OA为y轴,直线OB为x轴建直角坐标系.
由于抛物线的顶点是(6,4),
所以设抛物线的表达式为y=a(x-6)2+4,
当x=0,y=1时,1=a(0-6)2+4,
所以a=-$\frac{1}{12}$,
所以抛物线解析式为:y=-$\frac{1}{12}$x2+x+1;
(2)令y=0,则-$\frac{1}{12}$x2+x+1=0,
解得:x1=6-4$\sqrt{3}$(舍去),x2=6+4$\sqrt{3}$=12.8(米),
所以,足球落地点C距守门员约12.8米.
点评 此题主要考查了顶点式求二次函数解析式以及一元二次方程的解法等知识,正确建立坐标系得出解析式是解题关键.

练习册系列答案
相关题目
17. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③-1≤a≤-$\frac{2}{3}$;④4ac-b2>8a;
其中正确的结论是( )
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:①当x>3时,y<0;②3a+b<0;③-1≤a≤-$\frac{2}{3}$;④4ac-b2>8a;
其中正确的结论是( )
| A. | ①③④ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
15.下列图案中既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.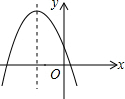 抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )
抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )
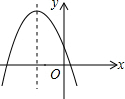 抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )
抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )| A. | 一、三象限 | B. | 一、二象限 | C. | 二、三象限 | D. | 二、四象限 |