题目内容
10．解方程1-$\frac{x+1}{3}$=$\frac{x}{2}$，去分母，得（ ）| A． | 1-2x-2=3x | B． | 6-2x+2=3x | C． | 6-2x-2=3x | D． | 6-3x-3=2x |
分析 方程左右两边乘以6去分母得到结果，即可作出判断．
解答 解：去分母得：6-2（x+1）=3x，
去括号得：6-2x-2=3x，
故选C
点评 此题考查了解一元一次方程，熟练掌握等式的性质及去括号法则是解本题的关键．
练习册系列答案
相关题目
20．
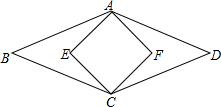如图，菱形ABCD的面积为120cm2，正方形AECF的面积为50cm2，则AB的长为（ ）
如图，菱形ABCD的面积为120cm2，正方形AECF的面积为50cm2，则AB的长为（ ）| A． | 9cm | B． | 12cm | C． | 13cm | D． | 15cm |
1．已知关于x的一元二次方程x2-3x+m=0的一个根为1，则m的值为（ ）
| A． | 2 | B． | -2 | C． | 4 | D． | -4 |
18．
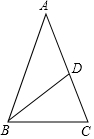如图，等腰三角形ABC中，AB=AC，BD平分∠ABC，∠A=36°，则∠BDC的度数为（ ）
如图，等腰三角形ABC中，AB=AC，BD平分∠ABC，∠A=36°，则∠BDC的度数为（ ）| A． | 36° | B． | 60° | C． | 108° | D． | 72° |
5．我县某乡镇冬枣园2014年产量为1000吨，2016年产量为1440吨，求该冬枣园冬枣产量的年平均增长率，设该冬枣园冬枣产量的年平均增长量为x，则根据题意可列方程为（ ）
| A． | 1440（1-x）2=1000 | B． | 1000（1-x）2=1440 | C． | 1440（1+x）2=1000 | D． | 1000（1+x）2=1440 |
10．
如图，边长12的正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在AB、BC、FD上．若BF=3，则小正方形的边长为多长？（ ）
如图，边长12的正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在AB、BC、FD上．若BF=3，则小正方形的边长为多长？（ ）| A． | 2$\sqrt{3}$ | B． | 3.75 | C． | 5 | D． | 6 |
8．
如图，是直立在高速公路边水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，则警示牌的高CD为（ ）
如图，是直立在高速公路边水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，则警示牌的高CD为（ ）| A． | 4$\sqrt{3}$米 | B． | （2$\sqrt{3}$+2）米 | C． | （4$\sqrt{2}$-4）米 | D． | （4$\sqrt{3}$-4）米 |