题目内容
5．我县某乡镇冬枣园2014年产量为1000吨，2016年产量为1440吨，求该冬枣园冬枣产量的年平均增长率，设该冬枣园冬枣产量的年平均增长量为x，则根据题意可列方程为（ ）| A． | 1440（1-x）2=1000 | B． | 1000（1-x）2=1440 | C． | 1440（1+x）2=1000 | D． | 1000（1+x）2=1440 |
分析 根据2016年的产量=2014年的产量×（1+年平均增长率）2，把相关数值代入即可．
解答 解：设该冬枣园产量的年平均增长率为x，则2015年的产量为1000（1+x）吨，2016年的产量为1000（1+x）（1+x）=1000（1+x）2吨，
根据题意，得1000（1+x）2=1440，
故选：D．
点评 本题考查了由实际问题抽象出一元二次方程，得到2016年产量的等量关系是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
15．已知|m+3|与（n-2）2互为相反数，那么mn等于（ ）
| A． | 6 | B． | -6 | C． | 9 | D． | -9 |
16．
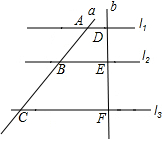如图，直线l1∥l2∥l3，且分别交直线a，b于点A、B、C、D、E、F，若AB=2，BC=3，DE=1，则EF的长为（ ）
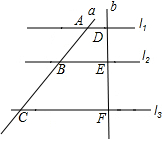如图，直线l1∥l2∥l3，且分别交直线a，b于点A、B、C、D、E、F，若AB=2，BC=3，DE=1，则EF的长为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | 6 | D． | $\frac{1}{6}$ |
13．某款服装按原售价提价a元后，再降价20%，现在售价为b元，则原售价为（ ）
| A． | （$\frac{5}{4}$b+a）元 | B． | （$\frac{5}{4}$b+a）元 | C． | （a+b）元 | D． | （$\frac{5}{4}$a+b）元 |
20．
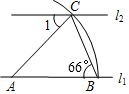如图，直线l1∥l2，以直线l1上的点A为圆心，适当长为半径画弧，分别交直线l1、l2于点B、C，连接AC、BC，若∠ABC=66°，则∠1=（ ）
如图，直线l1∥l2，以直线l1上的点A为圆心，适当长为半径画弧，分别交直线l1、l2于点B、C，连接AC、BC，若∠ABC=66°，则∠1=（ ）| A． | 23° | B． | 46° | C． | 66° | D． | 48° |
10．解方程1-$\frac{x+1}{3}$=$\frac{x}{2}$，去分母，得（ ）
| A． | 1-2x-2=3x | B． | 6-2x+2=3x | C． | 6-2x-2=3x | D． | 6-3x-3=2x |
2．
下列图形中有可能与图相似的是（ ）
下列图形中有可能与图相似的是（ ）| A． |  | B． |  | C． |  | D． |  |
3．单项式-9x3yz2的系数与次数的和是（ ）
| A． | 4 | B． | -3 | C． | -5 | D． | -6 |