题目内容
 2010年10月26日,沪杭高铁正式通车营运,甲乙两列高速列车在A,B两地之间匀速运行,两车离A地的距离s(千米)随时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:
2010年10月26日,沪杭高铁正式通车营运,甲乙两列高速列车在A,B两地之间匀速运行,两车离A地的距离s(千米)随时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:(1)A、B两地之间的距离为多少千米?
(2)甲车出发多长时间后被乙车追上?
(3)乙车的速度为多少?
考点:一次函数的应用
专题:
分析:(1)直接利用图象得出S的值,即可得出答案;
(2)首先求出甲所在直线解析式,进而得出相遇时的时间;
(3)利用图象得出乙行驶的时间与距离,进而得出其速度.
(2)首先求出甲所在直线解析式,进而得出相遇时的时间;
(3)利用图象得出乙行驶的时间与距离,进而得出其速度.
解答:解:(1)由图象可得出:A、B两地之间的距离为150千米;
(2)设直线甲的解析式为:y=kx,
将(45,150),代入得出:
y=
x,
当y=50,x=15,
即甲车出发15分钟后被乙车追上;
(3)由图象可得出:乙晚出发5分钟,即乙行驶50km,需要15-5=10(分钟),
故亿的速度为:
=300(km/h).
(2)设直线甲的解析式为:y=kx,
将(45,150),代入得出:
y=
| 10 |
| 3 |
当y=50,x=15,
即甲车出发15分钟后被乙车追上;
(3)由图象可得出:乙晚出发5分钟,即乙行驶50km,需要15-5=10(分钟),
故亿的速度为:
| 50 | ||
|
点评:此题主要考查了一次函数的应用,根据图象得出正确信息是解题关键.

练习册系列答案
相关题目
已知点O是△ABC的外心,且∠ABC+∠ACB=100°,则∠BOC=( )
| A、100° |
| B、100°或80° |
| C、130° |
| D、160° |
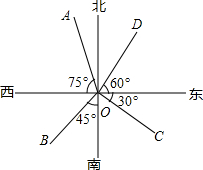 如图所示,对图中各射线表示的方向下列判断错误的是( )
如图所示,对图中各射线表示的方向下列判断错误的是( )| A、射线OA的方向是北偏西15° |
| B、射线OB的方向是南偏西45° |
| C、射线OC的方向是南偏东60° |
| D、射线OD的方向是北偏东60° |
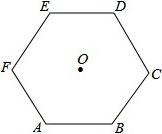 如图,O是正六边形ABCDEF的中心,半径为Rcm,求它的周长L和面积S.
如图,O是正六边形ABCDEF的中心,半径为Rcm,求它的周长L和面积S. 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.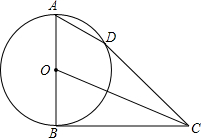 如图,已知AB是⊙O的直径,点D在⊙O上,C是⊙O外一点.若AD∥OC,直线BC与⊙O相交,判断直线CD与⊙O的位置关系,并说明理由.
如图,已知AB是⊙O的直径,点D在⊙O上,C是⊙O外一点.若AD∥OC,直线BC与⊙O相交,判断直线CD与⊙O的位置关系,并说明理由.