题目内容
10.不等式组$\left\{\begin{array}{l}{x+5≥0}\\{2-x>0}\end{array}\right.$的解集在数轴上表示为( )| A. |  | B. |  | ||
| C. |  | D. |  |
分析 分别求出不等式组中两不等式的解集,找出解集的公共部分即为不等式组的解集,表示在数轴上即可.
解答 解:$\left\{\begin{array}{l}{x+5≥0①}\\{2-x>0②}\end{array}\right.$,
由①得:x≥-5,
由②得:x<2,
∴不等式组的解集为-5≤x<2,
表示在数轴上,如图所示,
故选C
点评 此题考查了解一元一次不等式组,以及在数轴上表示不等式的解集,求出不等式组的解集是解本题的关键.

练习册系列答案
相关题目
15.下列说法不正确的是( )
| A. | (-$\frac{1}{4}$)2的平方根是$±\frac{1}{4}$ | B. | -5是25的一个平方根 | ||
| C. | 0.9的算术平方根是0.3 | D. | $\root{3}{-27}$=-3 |
2. 如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
 如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )| A. | 逐渐变短 | B. | 先变短后变长 | C. | 先变长后变短 | D. | 逐渐变长 |
19.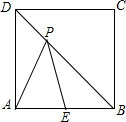 如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是( )
如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是( )
 如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是( )
如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{1}{2}$$+\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
20.计算:|-2|+20-(-1)2=( )
| A. | 2 | B. | 0 | C. | 1 | D. | 3 |
 如图是由5个大小相同的小正方体摆成的立体图形,它的左视图是( )
如图是由5个大小相同的小正方体摆成的立体图形,它的左视图是( )



 如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.求证:△APB≌△DPC.
如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.求证:△APB≌△DPC.