题目内容
7.已知关于x的方程x2+mx+m-2=0.(1)求证:不论m取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求该方程的另一根.
分析 (1)由方程的各系数结合根的判别式可得出△=(m-2)2+4>0,由此即可证出结论;
(2)将x=1代入原方程,得出关于m的一元一次方程,解方程求出m的值,将其代入原方程得出关于x的一元二次方程,结合根与系数的关系找出x1+x2=-$\frac{b}{a}$=-$\frac{1}{2}$,由此即可得出方程的另一根.
解答 (1)证明:∵在关于x的方程x2+mx+m-2=0中:△=m2-4×1×(m-2)=m2-4m+8=(m-2)2+4>0,
∴不论m取何实数,该方程都有两个不相等的实数根.
(2)解:将x1=1代入方程x2+mx+m-2=0中得:
1+m+m-2=0,解得:m=$\frac{1}{2}$.
∴原方程为x2+$\frac{1}{2}$x-$\frac{3}{2}$=0,
∴x1+x2=-$\frac{b}{a}$=-$\frac{1}{2}$,
∵x1=1,
∴x2=-$\frac{3}{2}$.
故若该方程的一个根为1,该方程的另一根为-$\frac{3}{2}$.
点评 本题考查了根的判别式、解一元一次方程以及根与系数的关系,解题的关键是:(1)找出△=(m-2)2+4>0;(2)求出m的值.本题属于基础题,难度不大,解决该题型题目时,根据根的判别式的符号判断根的个数是关键.

练习册系列答案
相关题目
17. 如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
 如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )| A. | 70° | B. | 100° | C. | 140° | D. | 170° |
15.下列说法不正确的是( )
| A. | (-$\frac{1}{4}$)2的平方根是$±\frac{1}{4}$ | B. | -5是25的一个平方根 | ||
| C. | 0.9的算术平方根是0.3 | D. | $\root{3}{-27}$=-3 |
2. 如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
 如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )| A. | 逐渐变短 | B. | 先变短后变长 | C. | 先变长后变短 | D. | 逐渐变长 |
19.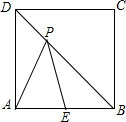 如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是( )
如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是( )
 如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是( )
如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{1}{2}$$+\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
 如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.求证:△APB≌△DPC.
如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.求证:△APB≌△DPC.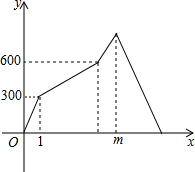 老王乘坐7:00的高铁从A地去B地开会,出发后发现一份重要的文件未带,让同事小李乘坐8:00的动车将文件送至B地.因火车会车原因,动车在途中停留了半小时.若高铁与动车的行驶路线相同、行驶过程中两车都以各自的速度匀速行驶,且A地到B地的全线长为1350千米.设高铁出发时间为t小时,高铁与动车的距离为y千米,y与t的函数图象如图所示.(注:高铁出发时,动车在A地;高铁到达B地后进行补给,直至动车到达B地.)
老王乘坐7:00的高铁从A地去B地开会,出发后发现一份重要的文件未带,让同事小李乘坐8:00的动车将文件送至B地.因火车会车原因,动车在途中停留了半小时.若高铁与动车的行驶路线相同、行驶过程中两车都以各自的速度匀速行驶,且A地到B地的全线长为1350千米.设高铁出发时间为t小时,高铁与动车的距离为y千米,y与t的函数图象如图所示.(注:高铁出发时,动车在A地;高铁到达B地后进行补给,直至动车到达B地.)