题目内容
4．
如图，四边形ABCD中，AB=CB，AD=CD，对角线AC，BD相交于点O，OE⊥AB，OF⊥CB，垂足分别是E、F．求证：OE=OF．
分析 欲证明OE=OF，只需推知BD平分∠ABC，所以通过全等三角形△ABD≌△CBD（SSS）的对应角相等得到∠ABD=∠CBD，问题就迎刃而解了．
解答 证明：∵在△ABD和△CBD中，$\left\{\begin{array}{l}{AB=CB}\\{AD=CD}\\{BD=BD}\end{array}\right.$，
∴△ABD≌△CBD（SSS），
∴∠ABD=∠CBD，
∴BD平分∠ABC．
又∵OE⊥AB，OF⊥CB，
∴OE=OF．
点评 本题考查了全等三角形的判定与性质．在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
如图，如果圆内接四边形ABCD两组对边的延长线分别相交于点E，F，且∠E=40°，∠F=60°，那么∠A=40°．
15．下列说法不正确的是（ ）
| A． | （-$\frac{1}{4}$）2的平方根是$±\frac{1}{4}$ | B． | -5是25的一个平方根 | ||
| C． | 0.9的算术平方根是0.3 | D． | $\root{3}{-27}$=-3 |
19．
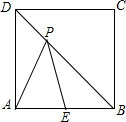如图，P是边长为1的正方形ABCD的对角线BD上的一点，点E是AB的中点，则PA+PE的最小值是（ ）
如图，P是边长为1的正方形ABCD的对角线BD上的一点，点E是AB的中点，则PA+PE的最小值是（ ）| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{\sqrt{6}}{2}$ | C． | $\frac{1}{2}$$+\frac{\sqrt{2}}{2}$ | D． | $\sqrt{2}$ |
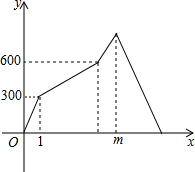老王乘坐7：00的高铁从A地去B地开会，出发后发现一份重要的文件未带，让同事小李乘坐8：00的动车将文件送至B地．因火车会车原因，动车在途中停留了半小时．若高铁与动车的行驶路线相同、行驶过程中两车都以各自的速度匀速行驶，且A地到B地的全线长为1350千米．设高铁出发时间为t小时，高铁与动车的距离为y千米，y与t的函数图象如图所示．（注：高铁出发时，动车在A地；高铁到达B地后进行补给，直至动车到达B地．）
13．下列分式中，最简分式是（ ）
| A． | $\frac{{3{x^2}}}{4xy}$ | B． | $\frac{{{x^2}+{y^2}}}{x+y}$ | C． | $\frac{x-2}{{{x^2}-4}}$ | D． | $\frac{1+x}{{{x^2}+2x+1}}$ |