Question

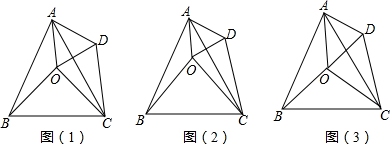
18．如图（1），点O是等边△ABC内一点，将△AOB绕点A逆时针旋转60°得△ADC，连接OD．
（1）求证：△DOA是等边三角形；
（2）如图（2），当∠AOB=150°时，判断△COD的形状，并说明理由；
（3）如图（3），当∠AOB=110°时，探究：当∠COB为多少度时，△COD是等腰三角形．

Answer 1

分析 （1）根据旋转的性质得AO=AD，∠OAD=60°，则根据等边三角形的判定方法可判断△DOA为等边三角形；
（2）根据旋转的性质得∠ADC=∠AOB=150°，再由△DOA为等边三角形得到∠ADO=60°，则可计算出∠ODC=∠ADC-∠ADO=90°，于是可判断△COD为直角三角形；
（3）由△DOA为等边三角形得到∠AOD=60°，而∠ODC=∠ADC-∠ADO=50°，然后分类讨论：当OD=OC时，根据等腰三角形的性质得∠OCD=∠ODC=50°，则根据三角形内角和可计算出∠DOC=80°，然后利用周角定义可计算出∠BOC=110°；当CO=CD时，则∠DOC=∠OCD=50°，则根据三角形内角和可计算出∠BOC=140°；当DO=DC时，∠DOC=∠DCO，根据三角形内角和得到∠DOC=65°，则根据三角形内角和可计算出∠BOC=125°．

解答 （1）证明：∵△AOB绕点A逆时针旋转60°得△ADC，
∴AO=AD，∠OAD=60°，
∴△DOA为等边三角形；
（2）解：△COD为直角三角形．理由如下：
∵△AOB绕点A逆时针旋转60°得△ADC，
∴∠ADC=∠AOB=150°，
∵△DOA为等边三角形，
∴∠ADO=60°，
∴∠ODC=∠ADC-∠ADO=150°-60°=90°，
∴△COD为直角三角形；
（3）解：∵△DOA为等边三角形，
∴∠AOD=60°，
∵∠ADC=∠AOB=110°，∠ADO=60°，
∴∠ODC=∠ADC-∠ADO=110°-60°=50°，
当OD=OC时，∠OCD=∠ODC=50°，则∠DOC=180°-50°-50°=80°，所以∠BOC=360°-∠AOB-∠AOD-∠DOC=360°-110°-60°-80°=110°；
当CO=CD时，∠DOC=∠OCD=50°，所以∠BOC=360°-∠AOB-∠AOD-∠DOC=360°-110°-60°-50°=140°；
当DO=DC时，∠DOC=∠DCO，则∠DOC=$\frac{1}{2}$（180°-50°）=65°，所以∠BOC=360°-∠AOB-∠AOD-∠DOC=360°-110°-60°-65°=125°；
综上所述，当∠COB为110°或125°或140°时，△COD是等腰三角形．

点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等边三角形的判定与性质和等腰三角形的性质．