题目内容
19.观察下列各式,用不等号连接起来52+32>2×5×3 22+12>2×2×1 22+22=2×2×2
($\frac{1}{2}$)2+($\frac{1}{3}$)2>2×$\frac{1}{2}$×$\frac{1}{3}$
试将上述各式用一个含有a、b的代数式表示其规律,并说明规律的正确性.
分析 先根据有理数的乘法和乘方法则进行计算,然后比较大小,总结规律,再用完全平方公式进行证明即可.
解答 解:52+32>2×5×3,22+12>2×2×1,22+22=2×2×2,($\frac{1}{2}$)2+($\frac{1}{3}$)2>2×$\frac{1}{2}$×$\frac{1}{3}$,
规律:a2+b2≥2ab.
证明:∵(a+b)2≥0,
∴a2+b2≥2ab.
点评 本题是通过数字的计算、比较,总结规律,属于中档题,关键是找出两个数的平方和与这两个数的积的2倍之间的大小关系,证明时,根据一个数或式的平方的非负性变形即可.

练习册系列答案
相关题目
7.在一个三角形中,已知AB=AC=6cm,BC=8cm,D是BC的中点,以D为圆心作一个半径为5cm的圆,则下列说法正确的是( )
| A. | 点A在⊙D外 | B. | 点B在⊙D上 | C. | 点C在⊙D内 | D. | 无法确定 |
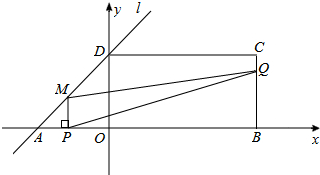 如图,在平面直角坐标系中,四边形ABCD是一个面积为48的直角梯形,∠C=90°,∠DAO=45°,AB∥CD,点B(10,0)直线l经过点A,D两点,且动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒4个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
如图,在平面直角坐标系中,四边形ABCD是一个面积为48的直角梯形,∠C=90°,∠DAO=45°,AB∥CD,点B(10,0)直线l经过点A,D两点,且动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒4个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.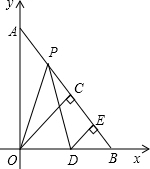 在△ABO中,∠AOB=90°,OA=OB=10,分别以边OA、OB所在的直线为坐标轴建立平面直角坐标系,点P自点A出发沿线段AB匀速运动至点B停止.同时点D自原点O出发沿x轴正方向匀速运动.在点P、D运动的过程中,始终满足PO=PD,过点O、D向直线AB做垂线,垂足分别为点C、E,设OD=x.
在△ABO中,∠AOB=90°,OA=OB=10,分别以边OA、OB所在的直线为坐标轴建立平面直角坐标系,点P自点A出发沿线段AB匀速运动至点B停止.同时点D自原点O出发沿x轴正方向匀速运动.在点P、D运动的过程中,始终满足PO=PD,过点O、D向直线AB做垂线,垂足分别为点C、E,设OD=x. 如图,矩形ABCD中,AB=6,BC=8,BC、BD上分别取点E、F,则CF+EF的最小值为7.68.
如图,矩形ABCD中,AB=6,BC=8,BC、BD上分别取点E、F,则CF+EF的最小值为7.68.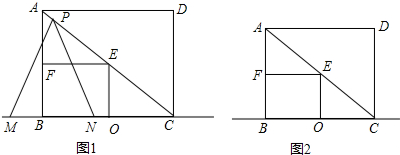
 如图,△ABC中,DE∥BC,AD=2,AE=3,BD=4,求AC的长.
如图,△ABC中,DE∥BC,AD=2,AE=3,BD=4,求AC的长.