题目内容
10.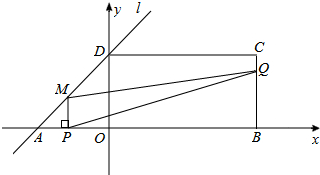 如图,在平面直角坐标系中,四边形ABCD是一个面积为48的直角梯形,∠C=90°,∠DAO=45°,AB∥CD,点B(10,0)直线l经过点A,D两点,且动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒4个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
如图,在平面直角坐标系中,四边形ABCD是一个面积为48的直角梯形,∠C=90°,∠DAO=45°,AB∥CD,点B(10,0)直线l经过点A,D两点,且动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒4个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P、Q两点中有一点到达终点时,另一点也随之停止运动,设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.(1)点A的坐标为(-4,0);直线l的解析式为y=x+4;
(2)试求点Q与点M的相遇前S与t的函数关系式,并写出相应的t的取值范围;
(3)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形,请直接写出t的值.
分析 (1)利用△AOD是等腰直角三角形,四边形ABCD是一个面积为48的直角梯形以及点B的坐标,求出OA=OD=4,即可确定点A的坐标为(-4,0),点D的坐标为(0,4),然后利用待定系数法可求出直线l的解析式;
(2)当点Q与点M的相遇时,可得2t-4=10-(4t-4),可求得t=3,然后分三种情况:0<t≤1,1<t≤2,2<t<3,分别利用图形的性质,三角形的面积公式进行分析解答即可;
(3)在△QMN中,∠QMN=90°,因此当MN=MQ时△QMN为等腰三角形.当2<t<3时,MQ=18-6t,OP=MN=DM=2t,进而由MN=MQ得到2t=18-6t,求出t的值;当3<t<3.5时,由于MN=DM>MQ,可知此种情况不成立.
解答 解:(1)(-4,0);y=x+4;
(2)根据题意,当点Q与点M的相遇时,可得2t-4=10-(4t-4),
解得t=3,即当t=3时,点Q与点M相遇.
分三种情况:
①当0<t≤1时,如题图,
此时AP=MP=2t,BP=AB-AP=14-2t,
∴S=$\frac{1}{2}$MP•BP=$\frac{1}{2}$•2t•(14-2t)=-2t2+14t;
②当1<t≤2时,如图1,
此时AP=MP=2t,CQ=4t-4,DQ=CD-CQ=10-(4t-4)=14-4t,
△MPQ的MP边上的高h为:h=AB-AP-CQ=14-2t-(4t-4)=18-6t,
∴S=$\frac{1}{2}$MP•h=$\frac{1}{2}$•2t(18-6t)=-6t2+18t;
③当2<t<3时,如图2,
此时MP=4,OP=DM=2t-4,CQ=4t-4,MQ=CD-DM-CQ=10-(2t-4)-(4t-4)=18-6t,
∴S=$\frac{1}{2}$MP•MQ=$\frac{1}{2}$×4•(18-6t)=-12t+36;
(3)在△QMN中,∠QMN=90°,因此当MN=MQ时△QMN为等腰三角形.
当2<t<3时,如图3,MQ=18-6t,OP=MN=DM=2t,
由MN=MQ可得2t=18-6t,
解得t=$\frac{11}{4}$;
当3<t<3.5时,如图4,
由于MN=DM>MQ,可知此种情况不成立.
所以t=$\frac{11}{4}$.
点评 本题考查了一次函数的综合应用,坐标与图形性质,直角梯形等知识,具有一定的综合性,解答本题时注意分类讨论思想、数形结合思想、方程思想的运用.

| A. | x•x3=x6 | B. | a2+a3=a5 | C. | (a3)2=a5 | D. | a3÷a=a2(a≠0) |
| A. | 0 | B. | -1 | C. | 1 | D. | 2 015 |
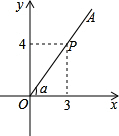 如图,P是∠α的边OA上一点,且P点的坐标为(3,4),则sin(90°-α)=$\frac{3}{5}$.
如图,P是∠α的边OA上一点,且P点的坐标为(3,4),则sin(90°-α)=$\frac{3}{5}$.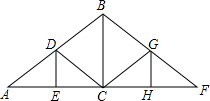 如图是屋架设计图的一部分,点D是斜梁AB的AB的中点,立柱BC、DE垂直于横梁AF.已知AB=12m,∠ADE=60°,则DE等于( )
如图是屋架设计图的一部分,点D是斜梁AB的AB的中点,立柱BC、DE垂直于横梁AF.已知AB=12m,∠ADE=60°,则DE等于( )