题目内容
将抛物线y=2(x+1)2+3关于y轴对称,得到的抛物线是( )
| A、y=2(x+1)2+3 |
| B、y=2(x-1)2+3 |
| C、y=2(x+1)2-3 |
| D、y=2(x-1)2-3 |
考点:二次函数图象与几何变换
专题:
分析:拋物线y=2(x+1)2+3顶点坐标为(-1,3),关于y轴对称后顶点坐标为(1,3),开口向上,可求该抛物线的解析式.
解答:解:∵拋物线y=2(x+1)2+3顶点坐标为(-1,3),关于y轴对称后顶点坐标为(1,3),且开口向上,
∴该抛物线的解析式为y=2(x-1)2+3;
故选:B.
∴该抛物线的解析式为y=2(x-1)2+3;
故选:B.
点评:本题考查了二次函数图象与几何变换.关键是根据顶点坐标的变换,由顶点式写出新抛物线的解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知直角三角形中一条直角边长为12cm,周长为30cm,则这个三角形的面积是( )
| A、20cm2 |
| B、30cm2 |
| C、60cm2 |
| D、75cm2 |
已知点A(4,3)和点B是坐标平面内的两个点,且它们关于过点(-3,0)与y轴平行的直线对称,则点B的坐标是( )
| A、(1,3) |
| B、(-10,3) |
| C、(4,3) |
| D、(4,1) |
下列方程中不是一元二次方程的是( )
| A、x2-6x=0 |
| B、9x2-6x=2x(4x+5) |
| C、3x2=5 |
| D、x(5x-2)=x(x+1)+4x2 |
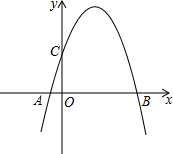 二次函数图象过A、C、B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且OB=OC.
二次函数图象过A、C、B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且OB=OC. 如图:AB=AD,∠BAD=∠CAE,要添加一个条件使△ABC≌△ADE,添加的条件可以是(只写一个)
如图:AB=AD,∠BAD=∠CAE,要添加一个条件使△ABC≌△ADE,添加的条件可以是(只写一个)