题目内容
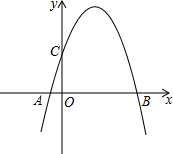二次函数图象过A、C、B三点，点A的坐标为（-1，0），点B的坐标为（4，0），点C在y轴正半轴上，且OB=OC．（1）求二次函数的解析式；
（2）该二次函数在第一象限的图象上有一动点为P，且点P在移动时满足S△PAB=10，求此时点P的坐标．
考点：待定系数法求二次函数解析式,二次函数的性质
专题：
分析：（1）根据A（-1，0），B（4，0），得OB=4，则OC=4，即点C的坐标为（0，4）．设图象经过A，C，B三点的二次函数的解析式为y=a（x-4）（x+1），根据点C（0，4）在图象上．可得出a=-1．从而得出所求的二次函数解析式为y=-（x-4）（x+1）．即y=-x2+3x+4．
（2）根据A、B的坐标求得AB的长，设P点的坐标为（x，-x2+3x+4），根据S△PAB=10，列出方程，解方程即可求得x的值，进而求得坐标．
（2）根据A、B的坐标求得AB的长，设P点的坐标为（x，-x2+3x+4），根据S△PAB=10，列出方程，解方程即可求得x的值，进而求得坐标．
解答：解：（1）∵A（-1，0），B（4，0），
∴OB=4，
∴OC=4，即点C的坐标为（0，4）．
设图象经过A，C，B三点的二次函数的解析式为y=a（x-4）（x+1），
∵点C（0，4）在图象上．
∴4=a（0-4）（0+1），即a=-1．
∴所求的二次函数解析式为y=-（x-4）（x+1）．
即y=-x2+3x+4，
故二次函数解析式为y=-x2+3x+4．
（2）∵点A的坐标为（-1，0），点B的坐标为（4，0），
∴AB=5，
设P点的坐标为（x，-x2+3x+4），
∵S△PAB=10，
∴
×5|-x2+3x+4|=10，
解得，x=3，或x=
，
∴P的坐标为（3，4）或（
，-4）．
∴OB=4，
∴OC=4，即点C的坐标为（0，4）．
设图象经过A，C，B三点的二次函数的解析式为y=a（x-4）（x+1），
∵点C（0，4）在图象上．
∴4=a（0-4）（0+1），即a=-1．
∴所求的二次函数解析式为y=-（x-4）（x+1）．
即y=-x2+3x+4，
故二次函数解析式为y=-x2+3x+4．
（2）∵点A的坐标为（-1，0），点B的坐标为（4，0），
∴AB=5，
设P点的坐标为（x，-x2+3x+4），
∵S△PAB=10，
∴
| 1 |
| 2 |
解得，x=3，或x=
3+
| ||
| 2 |
∴P的坐标为（3，4）或（
3+
| ||
| 2 |
点评：本题考查了用待定系数法求二次函数的解析式以及二次函数的性质，解答该题时，注意转化思想的应用．
练习册系列答案
相关题目
4600000用科学记数法表示，保留三个有效数字，结果是（ ）
| A、4.60×106 |
| B、4600000 |
| C、4.61×106 |
| D、4.605×106 |
如图所示，DE∥BC，AC=12，AD=下列说法中，不正确的是（ ）
| A、棱柱的侧面可以是三角形 |
| B、棱柱的侧面展开图是一个长方形 |
| C、若一个棱柱的底面为5边形、则可知该棱柱侧面是由5个长方形组成的 |
| D、棱柱的上底面与下底面的形状与大小是完全一样的 |
如图，正方形ABCD内接于⊙O，点P在弧AD上，则∠BPC=将抛物线y=2（x+1）2+3关于y轴对称，得到的抛物线是（ ）
| A、y=2（x+1）2+3 |
| B、y=2（x-1）2+3 |
| C、y=2（x+1）2-3 |
| D、y=2（x-1）2-3 |