题目内容
 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.将线段AB绕点B顺时针旋转90°,得线段A′B,点A的对应点为A′,连接AA′交线段BC于点D.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.将线段AB绕点B顺时针旋转90°,得线段A′B,点A的对应点为A′,连接AA′交线段BC于点D.(Ⅰ)作出旋转后的图形;
(Ⅱ)
| CD |
| DB |
考点:作图-旋转变换
专题:
分析:(1)根据图形旋转的性质画出图形即可;
(2)以点B为原点建立坐标系,利用待定系数法求出直线AA′及BC的直线方程,求出D点坐标,利用两点间的距离公式得出BD及CD的长,进而可得出其比值.
(2)以点B为原点建立坐标系,利用待定系数法求出直线AA′及BC的直线方程,求出D点坐标,利用两点间的距离公式得出BD及CD的长,进而可得出其比值.
解答: 解:(1)如图所示;
解:(1)如图所示;
(2)如图,以点B为原点建立坐标系,则A(-1,2),A′(2,1),C(2,2),B(0,0),
设直线AA′的解析式为y=kx+b(k≠0),
则
,
解得
,
故直线AA′的解析式为y=-
x+
;
∵C(2,2),B(0,0),
∴直线BC的解析式为y=x,
∴
,
解得
,
∴D(
,
),
∴DB=
=
,CD=
=
,
∴
=
=
.
故答案为:
.
 解:(1)如图所示;
解:(1)如图所示;(2)如图,以点B为原点建立坐标系,则A(-1,2),A′(2,1),C(2,2),B(0,0),
设直线AA′的解析式为y=kx+b(k≠0),
则
|
解得
|
故直线AA′的解析式为y=-
| 1 |
| 3 |
| 5 |
| 3 |
∵C(2,2),B(0,0),
∴直线BC的解析式为y=x,
∴
|
解得
|
∴D(
| 5 |
| 4 |
| 5 |
| 4 |
∴DB=
(
|
5
| ||
| 4 |
2(2-
|
3
| ||
| 4 |
∴
| CD |
| DB |
| ||||
|
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:本题考查的是作图-旋转变换,熟知图形旋转的性质是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
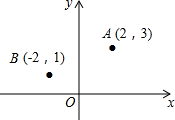 如图,在平面直角坐标系中,点A,B的坐标分别为(2,3),(2,1).
如图,在平面直角坐标系中,点A,B的坐标分别为(2,3),(2,1).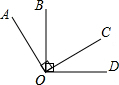 根据图,回答下列问题:
根据图,回答下列问题: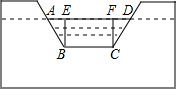 如图,利用土埂修筑一条渠道,在埂中间挖去深为0.6m的一块(图中的阴影部分),其横截面是梯形ABCD,其中,AB=CD,已知渠道内坡度为1:1.5,渠道地面宽BC为0.5m.
如图,利用土埂修筑一条渠道,在埂中间挖去深为0.6m的一块(图中的阴影部分),其横截面是梯形ABCD,其中,AB=CD,已知渠道内坡度为1:1.5,渠道地面宽BC为0.5m.
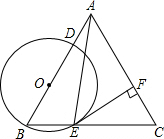 如图,在△ABC中,AB=AC,tanC=3,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.
如图,在△ABC中,AB=AC,tanC=3,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF. 已知:如图,△ABC和△ADE都是等边三角形.求证:∠ACD=∠ABE.
已知:如图,△ABC和△ADE都是等边三角形.求证:∠ACD=∠ABE.