题目内容
1．若a=2，b=3，则$\frac{{{a^2}+{b^2}-2ab}}{{{b^2}-ab}}$的值为$\frac{1}{3}$．分析 首先化简分式，进而将已知代入求出答案．
解答 解：$\frac{{{a^2}+{b^2}-2ab}}{{{b^2}-ab}}$=$\frac{（a-b）^{2}}{b（b-a）}$=$\frac{b-a}{b}$，
把a=2，b=3代入得：原式=$\frac{3-2}{3}$=$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．
点评 此题主要考查了分式的值，正确化简分式是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
11．下列各式中，是3x2y的同类项的是（ ）
| A． | 3a2b | B． | -2xy2 | C． | x2y | D． | 3xy |
为了解某小区家庭用水情况，小丽随机调查了该小区部分家庭4月份的用水量，并将收集的数据整理并绘制成如下条形统计图．
9．利用计算机设计了一个计算程序，输入和输出的数据如下表：
当输入的数据是8时，输出的数据是-$\frac{8}{65}$，当输入数据是n时，输出的数据是（-1）n+1$\frac{n}{{n}^{2}+1}$．
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | … | $\frac{1}{2}$ | $-\frac{2}{5}$ | $\frac{3}{10}$ | -$\frac{4}{17}$ | $\frac{5}{26}$ | … |
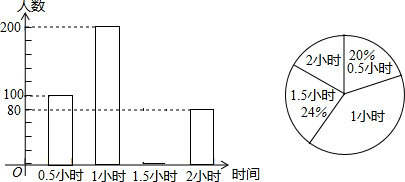
如图所示，?ABCD中，对角线AC，BD相交于点O，过点O的直线分别交AD、BC于点M，若△CON的面积为2，△DOM的面积为4，则?ABCD的面积为24．