题目内容
13.已知矩形纸片(如图1),AB=5,AD=4,用矩形纸片ABCD剪拼成一个无重叠无缝隙的正方形(1)写出剪拼成的正方形的边长;
(2)在图2的矩形ABCD中画出裁剪线,并在网格中画出用裁剪出的纸片拼成的正方形示意图(使正方形的顶点都在网格的格点上)
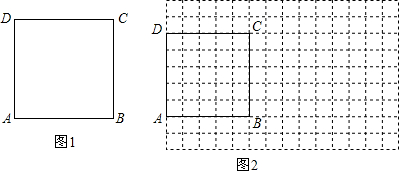
分析 (1)求得面积,再开方得出正方形的边长即可;
(2)利用求得的边长为$\sqrt{20}$=$\sqrt{16+4}$,裁剪出4个两条直角边分别为4、2的直角三角形,再把剩下的图形裁剪后拼接即可.
解答 解:(1)剪拼成的正方形的边长=$\sqrt{5×4}$=$\sqrt{20}$=2$\sqrt{5}$;
(2)如图,
点评 此题考查图形的剪拼,根据正方形的边长,明确分成的直角三角形的直角边为整数是解决问题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
18.在直角坐标系中,线段AB与x轴平行,则A、B两点坐标的特点是( )
| A. | 横坐标相同 | B. | 纵坐标相同 | ||
| C. | 横纵坐标都相同 | D. | 横纵坐标都不相同 |
 某市火车站开设了普通售票窗口和自动打印车票的无人售票窗口,某日从早上8时到上午11时,每个普通售票窗口售出车票数y1(张),每个无人售票窗口售出车票y2(张),如图所示,则上午11点,普通售票窗口开放5个,两种窗口共售出的车票数不少于2100张,无人售票窗口至少开放5个.
某市火车站开设了普通售票窗口和自动打印车票的无人售票窗口,某日从早上8时到上午11时,每个普通售票窗口售出车票数y1(张),每个无人售票窗口售出车票y2(张),如图所示,则上午11点,普通售票窗口开放5个,两种窗口共售出的车票数不少于2100张,无人售票窗口至少开放5个.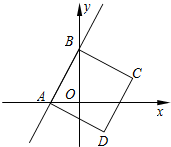 如图,一次函数y=2x+4的图象与x、y轴分别相交于点A和B,以AB为边作正方形ABCD.
如图,一次函数y=2x+4的图象与x、y轴分别相交于点A和B,以AB为边作正方形ABCD.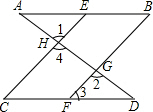 补全下列推理过程及括号内的推理依据:
补全下列推理过程及括号内的推理依据: