题目内容
1. 某市火车站开设了普通售票窗口和自动打印车票的无人售票窗口,某日从早上8时到上午11时,每个普通售票窗口售出车票数y1(张),每个无人售票窗口售出车票y2(张),如图所示,则上午11点,普通售票窗口开放5个,两种窗口共售出的车票数不少于2100张,无人售票窗口至少开放5个.
某市火车站开设了普通售票窗口和自动打印车票的无人售票窗口,某日从早上8时到上午11时,每个普通售票窗口售出车票数y1(张),每个无人售票窗口售出车票y2(张),如图所示,则上午11点,普通售票窗口开放5个,两种窗口共售出的车票数不少于2100张,无人售票窗口至少开放5个.
分析 直接利用待定系数法求一次函数解析式,利用设上午11点开放无人售票窗口a个,普通售票窗口5个,两种窗口共售出的车票数为2100张得出不等式求出即可.
解答 解:设y1=kx(k≠0),
把x=2,y=160代入解得:k=80,
所以y1=80x;
设y2=mx+n(m≠0),
把x=1.5,y=135;x=2,y=160代入得$\left\{\begin{array}{l}{1.5m+n=135}\\{2m+n=160}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=50}\\{n=60}\end{array}\right.$,
所以y2=50x+60;
设上午11点开放无人售票窗口a个,
由题意得(50×3+60)a+80×3×5≥2100,
解得x≥$\frac{30}{7}$.
所以上午11点无人售票窗口至少开放5个,
故答案为5.
点评 此题主要考查了一次函数的应用以及一元一次方程的应用等知识,表示出两种窗口共售出的车票数进而得出正确等量关系是解题关键.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
6.某大学生利用暑假参与一家旅行社的经营,了解到一条成本为500元/人的旅游线路的游客人数y(人/月)与旅游报价x(元/人)之间的关系如表:(旅游主管部门规定该旅游吸路线报价在800元/人~1500元/人之间)
(1)要将该旅游线路每月游客人数控制在200人以内(含200人),求该旅游线路报价的取值范围;
(2)求这条旅游线路所获得的利润w(元)与旅游报价x(元/人)之间的函数关系式.
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
| 旅游报价x元/人 | 游客人数y(人/月) |
| 800≤x<1200 | -x+1300 |
| 1200≤x<1500 | 100 |
(2)求这条旅游线路所获得的利润w(元)与旅游报价x(元/人)之间的函数关系式.
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
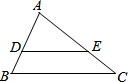 如图,在△ABC中,DE∥BC,$\frac{EC}{AE}$=$\frac{1}{2}$,△ADE的面积为8,则四边形DBCE的面积为( )
如图,在△ABC中,DE∥BC,$\frac{EC}{AE}$=$\frac{1}{2}$,△ADE的面积为8,则四边形DBCE的面积为( )