题目内容
17.如图在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+3与x轴交于点A,与y轴交于点B,直线l2:y=kx+2k与x轴交于点C,与直线l1交于点P.(1)直线l2是否经过x轴上一定点?若经过,请直接写出定点坐标;若不经过,请说明理由;
(2)若S△ACP=8,求直线l2的函数关系式;
(3)过点M(0,6)作平行于x轴的直线l3,点Q为直线l3上一个动点,当△QAB为等腰三角形时,求所有点Q的坐标.
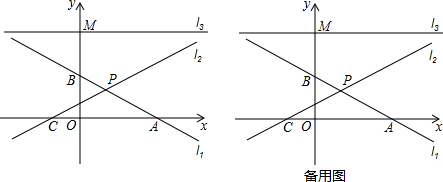
分析 (1)由y=kx+2k得到y=k(x+2),无论k取何值时,当x=-2时,y=0,故此直线y=kx+2k经过x轴上定点(-2,0);
(2)令y1=0得到-$\frac{1}{2}$x+3=0,解得x=6,故此A(6,0),由(1)可知点C的坐标为(-2,0),故此AC=8,由三角形的面积公式可知Py=2,将y=2代入y=-$\frac{1}{2}×$+3,求得x=2,于是得到点P的坐标为(2,2),将点P的坐标代入y=kx+2k可求得k的值;
(3)将x=0代入y=-$\frac{1}{2}$x+3得到y=3,从而得到点B的坐标为(0,3),设点Q的坐标为(n,6),分别根据QB=QA;BQ=BA;AB=AQ以及两点间的距离公式列出关于n的方程,从而可解得n的值.
解答 解:(1)∵y=kx+2k,
∴y=k(x+2).
∴当x=-2时,y=0.
∴直线L2经过点(-2,0).
(2)∵令y1=0得到-$\frac{1}{2}$x+3=0,解得x=6,
∴A(6,0).
∵由(1)可知:点C的坐标为(-2,0).
∴AC=8.
∵S△ACP=8,
∴$\frac{1}{2}×AC×{P}_{y}$=8,即$\frac{1}{2}×8×{P}_{y}$=8.
解得:Py=2.
∵将y=2代入-$\frac{1}{2}$x+3=0得:-$\frac{1}{2}$x+3=2,解得x=2,
∴点P的坐标为(2,2).
将点P的坐标代入y=kx+2k得:2k+2k=2,解得:k=$\frac{1}{2}$.
∴直线L2的解析式为$y=\frac{1}{2}x+1$.
(3)∵将x=0代入y=-$\frac{1}{2}$x+3得:y=3,
∴点B的坐标为(0,3).
设点Q的坐标为(n,6).
①当QB=QA时,由两点间的距离公式得:n2+(6-3)2=(6-n)2+(6-0)2.
解得:n=$\frac{21}{4}$.
∴点Q的坐标为($\frac{21}{4}$,6).
②当BQ=BA时,由两点间的距离公式得:n2+(6-3)2=(6-0)2+(3-0)2.
解得:n=6或n-6.
∴点Q的坐标为(6,6)或(-6,6).
∵将Q(-6,6)代入y=-$\frac{1}{2}x+3$得:y=-$\frac{1}{2}×$(-6)+3=6,
∴点Q在直线AB上,此时A、B、Q不能构成三角形.
∴Q(-6,6)(舍去).
∴点Q的坐标为(6,6).
③当AB=AQ时,由两点间的距离公式得:(n-6)2+(6-0)2=(6-0)2+(3-0)2.
解得:n=9或n=3.
∴点Q的坐标为(9,6)或(3,6).
综上所述,点Q的坐标为(9,6)或(3,6)或(6,6)或($\frac{21}{4},6$).
点评 本题主要考查的是一次函数的综合应用,解答本题主要应用了待定系数法求一次函数的解析式、一次函数图象上点的坐标特点、两点间的距离公式、等腰三角形的性质、三角形的面积公式,根据两点间的距离公式列出关于n的方程是解题的关键.

 如图,为了测量某栋大楼的高度AB,在D处用高为1米的测角仪CD测得大楼顶端A的仰角为30°,向大楼方向前进100米到达F处,又测得大楼顶端A的仰角为60°,则这栋大楼的高度AB(单位:米)为( )
如图,为了测量某栋大楼的高度AB,在D处用高为1米的测角仪CD测得大楼顶端A的仰角为30°,向大楼方向前进100米到达F处,又测得大楼顶端A的仰角为60°,则这栋大楼的高度AB(单位:米)为( )| A. | $50\sqrt{3}+1$ | B. | $50\sqrt{3}$ | C. | 51 | D. | 101 |
| A. | -a<0 | B. | a2>0 | C. | a2=-a2 | D. | a3=-a3 |
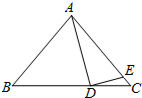 如图,在△ABC中,AB=AC,点D是BC上一点,点E是AC上一点,且DE⊥AD.若∠BAD=55°,∠B=50°,求∠DEC的度数.
如图,在△ABC中,AB=AC,点D是BC上一点,点E是AC上一点,且DE⊥AD.若∠BAD=55°,∠B=50°,求∠DEC的度数.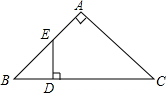 如图,在Rt△ABC中,∠A=90°,D为BC上一点,DC=AC,过点D作DE⊥BC交AB于点E,从图中找出与DE相等的线段,并证明.
如图,在Rt△ABC中,∠A=90°,D为BC上一点,DC=AC,过点D作DE⊥BC交AB于点E,从图中找出与DE相等的线段,并证明.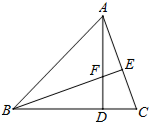 如图,锐角△ABC的高AD、BE相交于F,若BF=AC,BC=7,CD=2,则AF的长为3.
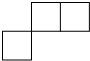
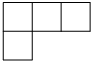
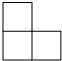
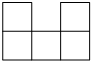
如图,锐角△ABC的高AD、BE相交于F,若BF=AC,BC=7,CD=2,则AF的长为3.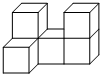 如图所示的几何体是由形状、大小都完全相同的小正方体组合而成的,则下列图形不可能是它的三视图的是( )
如图所示的几何体是由形状、大小都完全相同的小正方体组合而成的,则下列图形不可能是它的三视图的是( )