题目内容
5.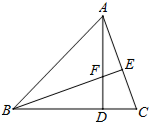 如图,锐角△ABC的高AD、BE相交于F,若BF=AC,BC=7,CD=2,则AF的长为3.
如图,锐角△ABC的高AD、BE相交于F,若BF=AC,BC=7,CD=2,则AF的长为3.
分析 先证出∠DBF=∠DAC,由AAS证明△BDF≌△ADC,得出对应边相等AD=BD=BC-CD=5,DF=CD=2,即可得出AF的长.
解答 解:∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
在△BDF与△ADC中,
$\left\{\begin{array}{l}{∠DBF=∠DAC}&{\;}\\{∠BDF=∠ADC}&{\;}\\{BF=AC}&{\;}\end{array}\right.$
∴△BDF≌△ADC(ASA),
∴AD=BD=BC-CD=7-2=5,DF=CD=2,
∴AF=AD-DF=5-2=3;
故答案为:3.
点评 本题考查了全等三角形的判定和性质;证明三角形的全等得出对应边相等是解此题的关键.

练习册系列答案
相关题目
4.已知∠A为锐角且tanA=$\sqrt{3}$,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 不能确定 |

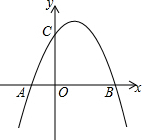 如图,已知c>0,抛物线y=-x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.
如图,已知c>0,抛物线y=-x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.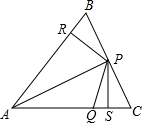 如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是①②④(请将所有正确结论的序号都填上).
如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是①②④(请将所有正确结论的序号都填上). 如图所示,AB+CD<AC+BD.(填“<”,“>”或“=”)
如图所示,AB+CD<AC+BD.(填“<”,“>”或“=”)