题目内容
如图，在△ABC中，∠A=30°，CA=10cm，以C为圆心、半径为5cm的圆与AB是什么位置关系？考点：直线与圆的位置关系
专题：
分析：过点C作CD⊥AB于点D，根据直角三角形的性质求出CD的长，再与5相比较即可得出结论．
解答：
解：过点C作CD⊥AB于点D，
∵在△ABC中，∠A=30°，CA=10cm，
∴CD=
CA=5cm，
∴半径为5cm的圆与AB相切．
解：过点C作CD⊥AB于点D，∵在△ABC中，∠A=30°，CA=10cm，
∴CD=
| 1 |
| 2 |
∴半径为5cm的圆与AB相切．
点评：本题考查的是直线与圆的位置关系，熟知设⊙O的半径为r，圆心O到直线l的距离为d，当d=r时，直线l和⊙O相切是解答此题的关键．
练习册系列答案
相关题目
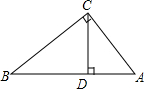如图，已知Rt△ABC中，∠C=90°，CD⊥AB于D，利用三角函数知识证明：
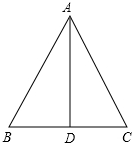如图，在△ABC中，AB=AC，AD是∠BAC的平分线，BD=2cm，求BC的长和∠ADC的大小．