题目内容
如图1所示，阴影部分是陆地，折线ABCDE是河岸，今要将河岸拉直，需在线段DE上找一点M，将河岸ABCDM变成线段AM，并且河面面积保持不变．
请你在图2中画出线段AM（保留作图痕迹），并说明理由．
请你在图2中画出线段AM（保留作图痕迹），并说明理由．
考点：作图—应用与设计作图
专题：
分析：首先连接BD，过C作CF∥BD交DE于F，利用三角形等底同高，则S△BDC=S△BDF．进而得出则S△AFB=S△AFM，连接AM即为所求．
解答：
解：连接BD，过C作CF∥BD交DE于F，
则S△BDC=S△BDF．
连接AF，过B作BM∥AF交DE于M，
则S△AFB=S△AFM，连接AM即为所求．
理由：∵S△BDC=S△BDF．
∴S△DQF=S△BQC，
∵S△AFB=S△AFM，
∴S△AGB=S△FGM，
∴S△DQF-S△FGM=S△BQC-S△AGB，
∴S△DQF-S△FGM=S△DRM-S△GQR，
S△BQC-S△AGB=S四边形TGQC-S△ABT，
∴S△DRM-S△GQR=S四边形TGQC-S△ABT，
∴S△DRM+S△ABT=S四边形TGQC+S△GQR．
∴河面面积保持不变．
解：连接BD，过C作CF∥BD交DE于F，则S△BDC=S△BDF．
连接AF，过B作BM∥AF交DE于M，
则S△AFB=S△AFM，连接AM即为所求．
理由：∵S△BDC=S△BDF．
∴S△DQF=S△BQC，
∵S△AFB=S△AFM，
∴S△AGB=S△FGM，
∴S△DQF-S△FGM=S△BQC-S△AGB，
∴S△DQF-S△FGM=S△DRM-S△GQR，
S△BQC-S△AGB=S四边形TGQC-S△ABT，
∴S△DRM-S△GQR=S四边形TGQC-S△ABT，
∴S△DRM+S△ABT=S四边形TGQC+S△GQR．
∴河面面积保持不变．
点评：此题主要考查了利用平行线间等底三角形面积关系以及设计作图应用，根据已知三角形面积关系得出AM是解题关键．
练习册系列答案
智能训练练测考系列答案
相关题目
若x2+3x-1=0，则x2+
的值为（ ）
| 1 |
| x2 |
| A、4 | B、7 | C、11 | D、-4 |
将直线y=-2x沿着y轴向下平移3个单位得到直线l，则直线l的解析式是（ ）
| A、y=-2x+3 |
| B、y=2x-3 |
| C、y=2x+3 |
| D、y=-2x-3 |
注意：为了使同学们更好地解答本题，我们提供了一种解题思路，你可以依照这个思路按下面的要求填空，完成本题的解答．也可以选用其他的解题方案，此时不必填空，只需按照解答题的一般要求进行解答．有一块长方形铁皮，长100cm，宽50cm，在它的四角各切去一个同样的正方形，然后将四周突出部分折起，就能制作一个无盖方盒．如果要制作的无盖方盒的底面积为3600cm2，那么铁皮各角应切去边长多大的正方形？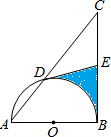
如图，以△ABC的直角边AB为直径的半圆O与斜边AC交于点D，E是BC边的中点．若AD、AB的长是方程x2-6x+8=0的两个根，则图中阴影部分的面积为