题目内容
11.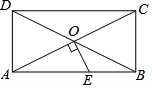 如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E.若BC=4,△AOE的面积为5,则BE=3.
如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E.若BC=4,△AOE的面积为5,则BE=3.
分析 首先连接EC,由题意可得OE为对角线AC的垂直平分线,可得CE=AE,S△AOE=S△COE=5,继而可得$\frac{1}{2}$AE•BC=10,则可求得AE的长,即EC的长,然后由勾股定理求得答案.
解答 解:连接EC.
由题意可得,OE为对角线AC的垂直平分线,
∴CE=AE,S△AOE=S△COE=5,
∴S△AEC=2S△AOE=10.
∴$\frac{1}{2}$AE•BC=10,
又∵BC=4,
∴AE=5,
∴EC=5.
在Rt△BCE中,由勾股定理得:BE=$\sqrt{C{E}^{2}-B{C}^{2}}$=3.
故答案为:3.
点评 此题考查了矩形的性质、勾股定理以及三角形的面积问题.此题难度适中,正确做出图形的辅助线是解题的关键.

练习册系列答案
相关题目
19.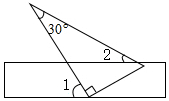 如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.若∠1=55°,则图中∠2的大小为( )
如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.若∠1=55°,则图中∠2的大小为( )
 如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.若∠1=55°,则图中∠2的大小为( )
如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.若∠1=55°,则图中∠2的大小为( )| A. | 25° | B. | 30° | C. | 35° | D. | 15° |
1.已知?ABCD中,∠B+∠D=200°,则∠A的度数为( )
| A. | 100° | B. | 160° | C. | 80° | D. | 60° |
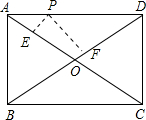 如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )
如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )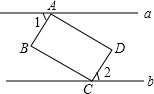 如图,矩形ABCD的顶点A、C分别在直线a、b上,且a与b平行,∠2=58°,则∠1的度数为58°.
如图,矩形ABCD的顶点A、C分别在直线a、b上,且a与b平行,∠2=58°,则∠1的度数为58°.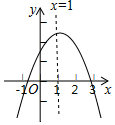 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的交点(x1,0),(x2,0),且-1<x1<0<x2,有下列5个结论:①abc<0;②b>a+c;③a+b>k(ka+b)(k为常数,且k≠1);④2c<3b;⑤若抛物线顶点坐标为(1,n),则b2=4a(c-n),其中正确的结论有( )个.
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的交点(x1,0),(x2,0),且-1<x1<0<x2,有下列5个结论:①abc<0;②b>a+c;③a+b>k(ka+b)(k为常数,且k≠1);④2c<3b;⑤若抛物线顶点坐标为(1,n),则b2=4a(c-n),其中正确的结论有( )个.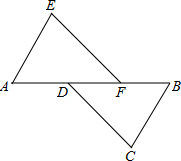 如图,A,D,F,B在同一直线上,AD=BF,AE=BC,且AE∥BC.
如图,A,D,F,B在同一直线上,AD=BF,AE=BC,且AE∥BC.