题目内容
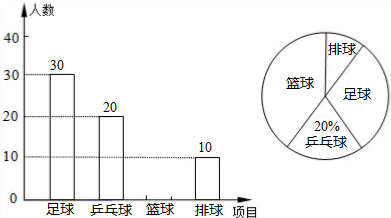
18.小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图.
请根据图中信息,解答下列问题.
(1)这次被调查的总人数是多少,并补全条形统计图.
(2)试求表示A组的扇形圆心角的度数.
(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比.
分析 (1)根据B类人数是19,所占的百分比是38%,据此即可求得调查的总人数,总人数减去A、B、D三组人数可得C组人数,补全图形;
(2)利用360°乘以对应的百分比即可求解;
(3)求得路程是6km时所用的时间,根据百分比的意义可求得路程不超过6km的人数所占的百分比.
解答 解:(1)19÷38%=50(人),
答:这次被调查的总人数是50人;
C组人数为:50-15-19-4=12(人),
补全条形统计图如图1:
(2)表示A组的扇形圆心角的度数为$\frac{15}{50}$×360°=108°;
答:A组的扇形圆心角的为108°;
(3)路程是6km时所用的时间是:6÷12=0.5(小时)=30(分钟),
则骑车路程不超过6km的人数所占的百分比是:$\frac{50-4}{50}$×100%=92%.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
6.某班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为x,按表格要求确定奖项.
(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
| 奖项 | 一等奖 | 二等奖 | 三等奖 |
| |x| | |x|=4 | |x|=3 | 1≤|x|<3 |
(2)是否每次抽奖都会获奖,为什么?
13.已知2a=-5b,则$\frac{a}{b}$的值为( )
| A. | $\frac{2}{5}$ | B. | -$\frac{2}{5}$ | C. | $\frac{5}{2}$ | D. | -$\frac{5}{2}$ |
8.不等式组$\left\{\begin{array}{l}2x<6\\ x+1≥-4\end{array}\right.$的解集是( )
| A. | -5≤x<3 | B. | -5<x≤3 | C. | x≥-5 | D. | x<3 |