题目内容
17.计算:(1)(a+2)2+(1-a)(1+a);
(2)[(x+y)2-(x-y)2]÷(2y).
分析 (1)根据完全平方公式和平方差公式对原式化简;
(2)根据完全平方公式和单项式除法可以对原式化简.
解答 解:(1)(a+2)2+(1-a)(1+a)
=a2+4a+4+1-a2
=4a+5;
(2)[(x+y)2-(x-y)2]÷(2y)
=[x2+2xy+y2-x2+2xy-y2]÷(2y)
=4xy÷(2y)
=2x.
点评 本题考查整式的混合运算,解题的关键是明整式的混合运算的计算方法.

练习册系列答案
相关题目
5.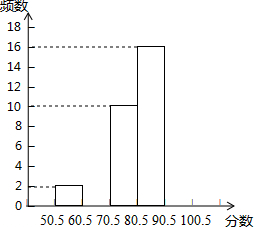 某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)
某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)
(1)频数分布表中A=80.5,B=16,C=0.2;
(2)补全频数分布直方图;
(3)若成绩在90分以上(不含90分)为优秀,试估计该校成绩优秀的有多少人?
 某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)
某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)| 分组 | 频数 | 频率 |
| 50.5~60.5 | 2 | 0.04 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | C |
| A~90.5 | B | 0.32 |
| 90.5~100.5 | 14 | 0.28 |
| 合计 |
(2)补全频数分布直方图;
(3)若成绩在90分以上(不含90分)为优秀,试估计该校成绩优秀的有多少人?
2.在实数:3.14159,$\root{3}{64}$,1.010010001…,$4.\stackrel{••}{21}$,π,$\frac{22}{7}$中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.某班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为x,按表格要求确定奖项.
(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
| 奖项 | 一等奖 | 二等奖 | 三等奖 |
| |x| | |x|=4 | |x|=3 | 1≤|x|<3 |
(2)是否每次抽奖都会获奖,为什么?
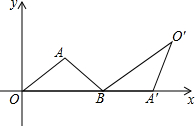 如图,把周长为22的△AOB放在平面直角坐标系中,OB在x轴的正半轴上,AO=AB=6,将△AOB绕点B按顺时针方向旋转一定角度后得到三角形A′O′B′,若点A的对应点A′在x轴上,则点O′的横坐标为$\frac{55}{3}$.
如图,把周长为22的△AOB放在平面直角坐标系中,OB在x轴的正半轴上,AO=AB=6,将△AOB绕点B按顺时针方向旋转一定角度后得到三角形A′O′B′,若点A的对应点A′在x轴上,则点O′的横坐标为$\frac{55}{3}$.