题目内容
3.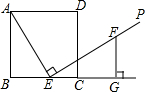 如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.
如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.(1)求证:FG=BE;
(2)探索点F是否在∠DCG的平分线上,并说明你的理由.
分析 (1)根据同角的余角相等得到一对角相等,再由一对直角相等,且AE=EF,利用AAS得到三角形ABE与三角形EFG全等,利用全等三角形的对应边相等即可得证;
(2)由(1)得到BC=AB=EG,利用等式的性质得到BE=CG,根据FG=BE,等量代价得到FG=CG,即三角形FCG为等腰直角三角形,得到∠FCG=45°,即可得证.
解答 (1)证明:∵EP⊥AE,
∴∠AEB+∠GEF=90°,
又∵∠AEB+∠BAE=90°,
∴∠GEF=∠BAE,
又∵FG⊥BC,
∴∠ABE=∠EGF=90°,
在△ABE与△EGF中,
$\left\{\begin{array}{l}{∠ABE=∠EGF}\\{∠BAE=∠GEF}\\{AE=EF}\end{array}\right.$,
∴△ABE≌△EGF(AAS),
∴FG=BE;
(2)解:点F在∠DCG的平分线上,理由如下:
连接CF,如图: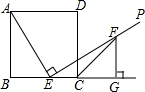
由(1)知:BC=AB=EG,
∴BC-EC=EG-EC,
∴BE=CG,
又∵FG=BE,
∴FG=CG,
又∵∠CGF=90°,
∴∠FCG=45°=$\frac{1}{2}$∠DCG,
∴CF平分∠DCG.
点评 此题属于四边形综合题,涉及的知识有:全等三角形的判定与性质,相似三角形的判定与性质,以及锐角三角函数定义,熟练掌握判定与性质是解本题的关键.

练习册系列答案
相关题目
13.若△ABC三边分别是a、b、c,且满足(b-c)(a2+b2)=bc2-c3,则△ABC是( )
| A. | 等边三角形 | B. | 等腰三角形 | ||
| C. | 直角三角形 | D. | 等腰或直角三角形 |
11.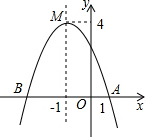 如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )
如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )
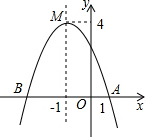 如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )
如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )| A. | a<0 | B. | 当x=-1时,函数y有最小值4 | ||
| C. | 对称轴是直线=-1 | D. | 点B的坐标为(-3,0) |
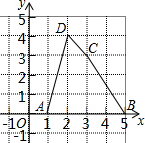 在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0),B(5,0),C(3,3),D(2,4).
在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0),B(5,0),C(3,3),D(2,4).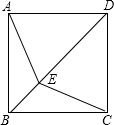 如图,在正方形ABCD中,点E是对角线BD上的点,求证:△ABE≌△CBE.
如图,在正方形ABCD中,点E是对角线BD上的点,求证:△ABE≌△CBE.